Wahrscheinlichkeitstheorie und Trading

Was ist die Wahrscheinlichkeitstheorie und warum ist sie wichtig?

Die Wahrscheinlichkeitstheorie ist für den Handel und das Investieren von entscheidender Bedeutung, da sie es den Marktteilnehmern ermöglicht, die Unsicherheit und das Risiko, die mit Finanzentscheidungen verbunden sind, zu verstehen und zu quantifizieren.

Wie das Leben selbst, geht es auch beim Trading um Wahrscheinlichkeiten. Es gibt selten offensichtliche, schwarz-weiße Ergebnisse, aus denen sich leicht Kapital schlagen lässt.

Durch die Anwendung der Wahrscheinlichkeitstheorie können Trader/Anleger auf der Grundlage der Wahrscheinlichkeit verschiedener Ergebnisse fundiertere Entscheidungen treffen.

Hier sind einige Gründe, warum die Wahrscheinlichkeitstheorie beim Trading/Investieren so wichtig ist :

Quantifizierung des Risikos

Mithilfe der Wahrscheinlichkeitstheorie können Anleger die Wahrscheinlichkeit berechnen, mit der verschiedene Dinge eintreten, einschließlich positiver und negativer Szenarien.

Dadurch können Trader die potenziellen Risiken, die mit verschiedenen Transaktionen/Investitionen verbunden sind, besser verstehen.

Entscheidungsfindung

Die Wahrscheinlichkeitstheorie ermöglicht es Händlern, bessere Entscheidungen zu treffen, indem sie sich auf die Wahrscheinlichkeit verschiedener Ergebnisse stützen und die Wahrscheinlichkeiten selbst bewerten (was man als "Wahrscheinlichkeiten von Wahrscheinlichkeiten" bezeichnen könnte, da die Chancen, dass verschiedene Dinge eintreten, selbst nicht bekannt sind).

Wenn z. B. eine Investition oder Transaktion mit einer Wahrscheinlichkeit von 70 % eine positive Rendite über ein Jahr erwirtschaftet, woher wissen Sie das?

Die Wahrscheinlichkeitstheorie umfasst Aspekte wie die Varianz und wie Sie besser mit dem umgehen können, was Sie nicht wissen und nicht wissen können.

Portfoliomanagement

Die Wahrscheinlichkeitstheorie hilft Händlern/Investoren bei der Verwaltung ihrer Portfolios, indem sie ihnen ein Mittel an die Hand gibt, um das mit verschiedenen Anlageklassen verbundene Risiko zu bewerten.

Indem sie die Wahrscheinlichkeit verschiedener Ergebnisse analysieren, können Händler/Investoren ein diversifiziertes Portfolio zusammenstellen, das Risiko und Ertrag in ein ausgewogenes Verhältnis bringt.

Risikomanagement

Die Wahrscheinlichkeitstheorie ist auch für das Risikomanagement wichtig, da sie den Anlegern hilft, die Wahrscheinlichkeit von Ereignissen zu bestimmen, die sich negativ auf ihre Investitionen/Transaktionen auswirken könnten, und Maßnahmen zu ergreifen, um diese Ereignisse abzumildern.

Insgesamt ist die Wahrscheinlichkeitstheorie ein wichtiges Instrument, das es Anlegern/Händlern ermöglicht, die Risiken und potenziellen Gewinne verschiedener Anlagemöglichkeiten zu verstehen, fundiertere Entscheidungen zu treffen und langfristig bessere Ergebnisse zu erzielen.

In diesem Artikel befassen wir uns mit den verschiedenen Zweigen der Wahrscheinlichkeitstheorie und ihren Anwendungen im Bereich des Tradings.

Zufall

In der Wahrscheinlichkeitstheorie bezieht sich die Zufälligkeit auf die Tatsache, dass der Ausgang eines Ereignisses nicht vorhersehbar ist und von Versuch zu Versuch variieren kann.

Dieses Phänomen wird häufig mithilfe von Wahrscheinlichkeitsverteilungen modelliert, die die Wahrscheinlichkeit jedes möglichen Ergebnisses beschreiben.

Zufälligkeit ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie, da es uns ermöglicht, das Unbekannte zu quantifizieren und aus unvollständigen Informationen Vorhersagen über die Zukunft zu treffen.

In vielen Situationen der realen Welt werden die Ergebnisse von Ereignissen von einer Vielzahl von Variablen beeinflusst, die sich nur schwer oder gar nicht mit Sicherheit/Genauigkeit vorhersagen lassen.

Mithilfe des Zufallsprinzips kann dies berücksichtigt und die Wahrscheinlichkeit verschiedener Ergebnisse auf der Grundlage historischer Daten, wirtschaftlicher Kausalzusammenhänge oder anderer Informationen geschätzt werden.

Beim Handeln und Investieren ist der Zufall immer präsent, da die Finanzmärkte einer Vielzahl von Einflüssen ausgesetzt sind.

Es gibt viele verschiedene Arten von Menschen auf den Märkten, die unterschiedlich groß sind und unterschiedliche Motivationen für ihre Transaktionen haben.

Die Zufälligkeit kann sich in Form von Marktvolatilität, unerwarteten Ereignissen oder anderen Faktoren äußern, die zu schnellen und unvorhersehbaren Kursschwankungen führen können.

Diese Zufälligkeit zu verstehen und zu berücksichtigen, ist für die Entwicklung erfolgreicher Handelsstrategien und das Risikomanagement von entscheidender Bedeutung.

Je mehr Erfahrung die Menschen auf den Märkten sammeln, desto mehr erkennen sie, dass alles, was sie wissen, im Vergleich zu den Dingen, die man aufgrund der Aktualität auf den Märkten wissen muss, gering ist.

Eine Möglichkeit, wie Händler und Investoren mit der Zufälligkeit umgehen können, besteht darin, wahrscheinlichkeitsbasierte Modelle für ihre Entscheidungen zu verwenden.

Beispielsweise kann ein Händler ein statistisches Modell verwenden, um die Wahrscheinlichkeit zu schätzen, dass der Preis eines bestimmten Vermögenswerts in einem bestimmten Zeitraum steigt oder fällt. Diese Informationen können dann verwendet werden, um ein gut ausgewogenes Portfolio zusammenzustellen und das Risiko zu steuern.

Wenn zum Beispiel die Verteilung der abgezinsten Preise eines bestimmten Vermögenswerts so aussieht:

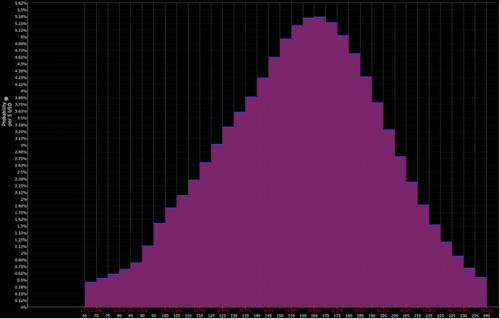
Und die Interpretation des Händlers entspricht eher der Kombination aus roter und violetter Verteilung (d. h. einer Abwärtsneigung) :

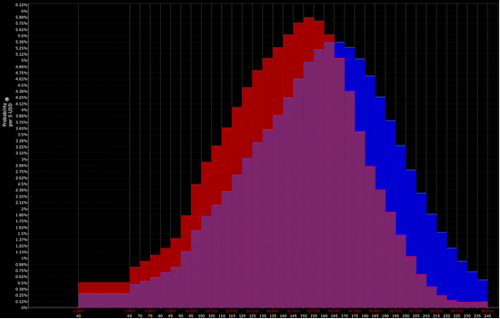
Dann können sie davon ausgehen, dass sie eine Baisse-Position auf den Vermögenswert einnehmen werden. Dann stellt sich natürlich die Frage, wie man sie umsetzt und wie groß sie ist.

Gegenseitige Ausschließlichkeit

In der Wahrscheinlichkeitstheorie bezieht sich das Konzept der gegenseitigen Exklusivität auf die Eigenschaft zweier Ereignisse, die sich voneinander unterscheiden.

Mathematisch werden zwei Ereignisse A und B als sich gegenseitig ausschließend bezeichnet, wenn ihr Schnittpunkt (d. h. das Ereignis, bei dem A und B beide eintreten) leer ist, d. h. P(A ∩ B) = 0.

Die gegenseitige Ausschließlichkeit ist beim Trading/Investment wichtig, da sie den Anlegern hilft, besser zu verstehen, wie sie ihre Risiken managen können.

Wenn Anleger ein Portfolio von Vermögenswerten halten, müssen sie die Korrelationen zwischen/unter ihren Vermögenswerten berücksichtigen.

Nehmen wir zum Beispiel an, dass ein Händler/Investor ein Aktienportfolio besitzt, das sowohl Technologie- als auch Ölunternehmen umfasst. Wenn der Ölpreis steigt, kann dies den Ölfirmen helfen, aber die Technologiewerte können darunter leiden (z. B. aufgrund der negativen Auswirkungen steigender Ölpreise auf die Zinssätze), und umgekehrt.

Wenn es jedoch in jedem Sektor zu bestimmten Entwicklungen kommt, haben diese möglicherweise keinen Einfluss auf die Kurse der Wertpapiere des anderen Sektors.

Selbst wenn also Wertpapiere in mancher Hinsicht miteinander verbunden sind - wie z. B. Veränderungen des diskontierten Wachstums und der Inflation -, schließen sie sich in anderer Hinsicht gegenseitig aus.

Wie werden diese sich gegenseitig ausschließenden Faktoren voneinander getrennt?

Manchmal geht es einfach um die Art des Finanzstroms - z. B. Öl im Vergleich zu technologischen Produkten/Dienstleistungen.

Manchmal werden sie als Faktoren bezeichnet - z. B. Momentum, Größe, Qualität, Wert etc.

Darüber hinaus ist die gegenseitige Exklusivität beim Optionshandel wichtig, wo der Gewinn einer Option oft auf dem Nichteintreten eines anderen Ereignisses beruhen kann. In diesem Zusammenhang hilft die gegenseitige Exklusivität den Händlern, ihre Risiken abzusichern und ihr Engagement zu steuern.

Experiment (Bernoulli-Versuch)

Ein Experiment oder ein Bernoulli-Versuch ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie, das sich auf ein zufälliges Ereignis mit nur zwei möglichen Ergebnissen bezieht.

Beispielsweise ist das Werfen einer Münze ein Bernoulli-Versuch, bei dem die möglichen Ergebnisse Kopf oder Zahl sind.

Ein anderes Beispiel ist die Frage, ob ein bestimmtes Optionsgeschäft bei seinem Ablauf zahlungswirksam (innerhalb des Kurses) oder nicht (außerhalb des Kurses) sein wird.

In der Wahrscheinlichkeitstheorie wird die Erfolgswahrscheinlichkeit (d. h. der Ausgang, der uns interessiert) durch p und die Misserfolgswahrscheinlichkeit (d. h. der andere Ausgang) durch q = 1 - p definiert.

Die Ergebnisse eines Bernoulli-Versuchs werden häufig mit 1 für Erfolg und 0 für Misserfolg bezeichnet.

Die Bedeutung der Bernoulli-Versuche im Bereich des Handels und der Investition liegt darin, dass einige Finanzentscheidungen binäre Ergebnisse beinhalten.

Beispielsweise können Sie sich entscheiden, eine Aktienoption zu kaufen, in der Hoffnung, dass sie den Break-even-Punkt erreicht, oder Sie können sich entscheiden, sie zu verkaufen, in der Hoffnung, dass ihr Preis den Break-even-Punkt erreicht und Sie die gesamte Prämie einnehmen.

In beiden Fällen ist das Ergebnis in Form von Geld binär. Reine Binärwetten werden in Form von binären Optionen angeboten.

Wenn Sie die Prinzipien der Wahrscheinlichkeitstheorie auf das Trading und Investieren anwenden, können Sie fundiertere Entscheidungen darüber treffen, wann Sie kaufen oder verkaufen sollten.

Es gibt auch Konzepte wie den Erwartungswert, die Sie lehren, nicht immer auf das wahrscheinlichste Ergebnis zu setzen.

Verteilung von Wahrscheinlichkeiten

In der Wahrscheinlichkeitstheorie ist eine Wahrscheinlichkeitsverteilung eine Funktion, die die Wahrscheinlichkeit verschiedener Ergebnisse in einem Zufallsexperiment oder -prozess beschreibt.

Sie gibt die Wahrscheinlichkeiten aller möglichen Ergebnisse eines Ereignisses an, wobei die Summe der Wahrscheinlichkeiten aller Ergebnisse gleich eins ist.

Es gibt viele verschiedene Arten von Wahrscheinlichkeitsverteilungen, aber zu den häufigsten gehören die Normalverteilung, die Binomialverteilung und die Poisson-Verteilung.

Jede Verteilung hat ihren eigenen Satz von Parametern, die ihre Form bestimmen, und diese Parameter werden häufig verwendet, um Vorhersagen zu treffen und Entscheidungen zu treffen.

Natürlich neigen Renditen auf den Finanzmärkten dazu, breitere Schwänze zu haben und nicht einer vorgegebenen Verteilung zu entsprechen, daher neigen sie dazu, individuell angepasst zu sein.

Insgesamt sind Wahrscheinlichkeitsverteilungen wichtig, da sie einen Rahmen für das Verständnis der mit Finanzinvestitionen verbundenen Risiken und Unsicherheiten bieten.

Eines der wichtigsten Konzepte im Bereich Trading/Investment ist, dass alles eine Wahrscheinlichkeit ist (d. h. eine Verteilung potenzieller Ergebnisse). Es gibt kein einziges Ergebnis, das besonders wahrscheinlich ist.

Durch die Verwendung von Wahrscheinlichkeitsverteilungen können Händler und Investoren die Wahrscheinlichkeit verschiedener Ergebnisse abschätzen und fundiertere Entscheidungen darüber treffen, wie sie ihre Ressourcen zuteilen.

Ein Händler könnte z. B. die Normalverteilung oder eine Verteilung mit dickerem Schwanz verwenden, um die täglichen Renditen einer bestimmten Aktie zu modellieren.

Er könnte dann diese Verteilung verwenden, um die Wahrscheinlichkeit zu schätzen, dass die Rendite der Aktie einen bestimmten Schwellenwert überschreitet, z. B. eine Rendite von +/-5 % an einem Tag.

Indem er Wahrscheinlichkeitsverteilungen auf diese Weise nutzt, kann der Händler sein Risiko besser steuern und seine Renditen optimieren.

Neben der Schätzung von Wahrscheinlichkeiten werden Wahrscheinlichkeitsverteilungen auch zur Erstellung von Finanzinstrumenten wie Optionen und Futures verwendet.

Der Preis dieser Instrumente basiert auf der zugrunde liegenden Verteilung des Vermögenswerts, an den sie gebunden sind, und Händler können sie zur Absicherung ihres Risikos verwenden oder Wetten auf zukünftige Preisbewegungen des Vermögenswerts abschließen.

Darüber hinaus können Ausschüttungen auf der Grundlage des Preises der zugrunde liegenden Optionen konstruiert werden, wie im Folgenden gezeigt wird.

Ausschüttung wie von den Märkten aktualisiert :

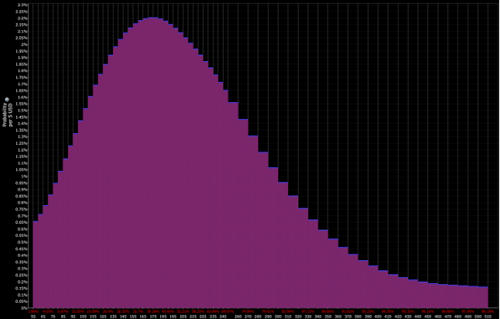
Vom Trader bestimmte Verteilung (was taktische Möglichkeiten eröffnet) :

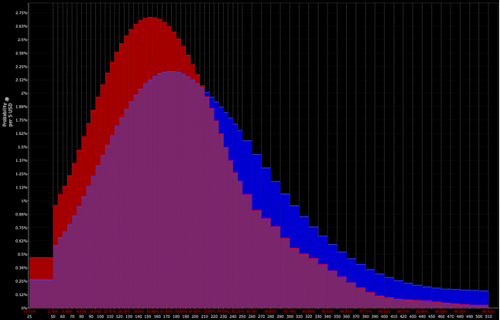
Binomialverteilung

Die Binomialverteilung ist eine Wahrscheinlichkeitsverteilung, die die Anzahl der positiven Ergebnisse in einer Reihe von unabhängigen und identischen Versuchen modelliert, wobei jeder Versuch nur zwei mögliche Ergebnisse hat (z. B. Kopf oder Zahl, Gewinner oder Verlierer, oben oder unten).

Die Schlüsselparameter der Binomialverteilung sind die Wahrscheinlichkeit, dass ein einzelner Versuch erfolgreich ist (bezeichnet als p), und die Anzahl der Versuche (bezeichnet als n).

Die Binomialverteilung ist im Bereich des Handels und der Investitionen wichtig, da sie zur Modellierung der Verteilung der Renditen einer binären Handelsstrategie verwendet werden kann (z. B. eine Strategie, bei der ein Vermögenswert gekauft oder verkauft wird, je nachdem, ob ein bestimmtes Ereignis eintritt oder nicht).

Insbesondere kann der Erwartungswert einer binären Handelsstrategie unter Verwendung der Binomialverteilung berechnet werden.

Der Erwartungswert einer binären Handelsstrategie ist die Summe der Produkte aus der Wahrscheinlichkeit jedes möglichen Ergebnisses und der diesem Ergebnis entsprechenden Rendite.

Wenn eine binäre Handelsstrategie zum Beispiel mit einer Wahrscheinlichkeit von 60% eine Rendite von 10% und mit einer Wahrscheinlichkeit von 40% eine Rendite von -5% erzielt, ist der Erwartungswert der Strategie wie folgt:

(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04

Die Binomialverteilung kann verwendet werden, um die Wahrscheinlichkeiten für jedes mögliche Ergebnis in einer Reihe von Binärgeschäften zu berechnen.

Wenn ein Händler beispielsweise 10 Binärgeschäfte mit einer Erfolgswahrscheinlichkeit von 60 % und einer Misserfolgswahrscheinlichkeit von 40 % durchführt, kann die Wahrscheinlichkeit, eine bestimmte Anzahl erfolgreicher Geschäfte (d. h. eine bestimmte Erfolgsquote) zu erzielen, mithilfe der Binomialverteilung berechnet werden.

Dies kann dem Trader helfen, das Risiko und die potenzielle Rendite seiner Handelsstrategie einzuschätzen.

Erwartungswert

Wir haben uns in anderen Artikeln mit dem Erwartungswert (ES) befasst, da es sich dabei um ein grundlegendes Konzept der Wahrscheinlichkeitstheorie handelt, das das durchschnittliche Ergebnis einer Zufallsvariablen beschreibt.

Im Bereich des Handels und der Investitionen wird der Erwartungswert zur Berechnung der potenziellen Rendite und des Risikos einer Investition oder Handelsstrategie verwendet.

Mathematisch gesehen ist der Erwartungswert einer Zufallsvariablen die Summe der Produkte aus jedem möglichen Ergebnis und seiner Wahrscheinlichkeit.

Nehmen wir zum Beispiel den Fall einer Münzauslosung, bei der die Köpfe 1 $ und die Schwänze 0 $ einbringen.

Der Erwartungswert dieser Münzauslosung ist wie folgt:

ES = (0,5 * $1) + (0,5 * $0) = $0,50.

Das bedeutet, dass der durchschnittliche Gewinn für diesen Münzwurf 0,50 $ beträgt. Auf diese Weise erhalten Sie im Laufe der Zeit eine Gewinnschwelle, da Ihre Chancen der tatsächlichen Wahrscheinlichkeit entsprechen.

Beim Handeln und Investieren wird der Erwartungswert verwendet, um die potenziellen Renditen einer Handelsstrategie oder einer Investition abzuschätzen.

Wenn eine Aktie beispielsweise eine 60%ige Chance hat, ihren Wert um 10% zu erhöhen, und eine 40%ige Chance hat, ihn um 5% zu senken, kann die erwartete Rendite der Investition wie folgt berechnet werden:

ES = (0,6 * 10%) + (0,4 * -5%) = 6% - 2% = 4%.

Das bedeutet, dass die erwartete Rendite der Investition 4 % beträgt.

Diese Informationen können Anlegern und Händlern bei der Entscheidung helfen, in die Aktie zu investieren und das Risiko und die potenzielle Rendite ihrer Investition einzuschätzen.

Der Erwartungswert ist auch für das Risikomanagement wichtig.

Durch die Berechnung des Erwartungswerts einer Handelsstrategie oder einer Investition können Händler und Investoren das potenzielle Risiko der Investition einschätzen.

Wenn der Erwartungswert einer Investition beispielsweise negativ ist, bedeutet dies, dass die Investition im langfristigen Durchschnitt wahrscheinlich Geld verlieren wird.

Händler/Investoren können diese Informationen nutzen, um ihr Risiko zu steuern, indem sie ihre Investitionen diversifizieren oder ihr Engagement für die Investition oder Transaktion begrenzen.

Darüber hinaus ist es, wie wir auch in anderen Artikeln behandelt haben, nicht immer die beste Entscheidung, auf das Ergebnis mit dem höchsten Erwartungswert zu wetten.

Manchmal ist es besser, einen niedrigeren Erwartungswert zu haben, wenn Sie dadurch eine geringere Varianz haben (geringeres Risiko eines Verlusts oder Misserfolgs). Außerdem wollen Sie immer sicherstellen, dass Sie den Verlust decken können.

Wenn Sie beispielsweise 1.000 $ zur Verfügung haben und eine 90%ige Chance haben, Ihr Geld auf 2.000 $ zu verdoppeln, und eine 10%ige Chance haben, die gesamten 1.000 $ zu verlieren, ist Ihr VA sehr hoch (1.800 $ - 1.000 $ = +800 $).

Wenn Sie es sich aber nicht leisten können, die 1.000 $ zu verlieren, falls Sie sich irren, sollten Sie die Entscheidung lieber nicht treffen.

Markov-Kette

Die Markov-Kette ist ein mathematisches Konzept aus der Wahrscheinlichkeitstheorie, das einen Prozess beschreibt, bei dem der nächste Schritt oder Zustand nur vom aktuellen Zustand und nicht von den vorherigen Zuständen abhängt.

Mit anderen Worten: Es handelt sich um einen Prozess ohne Gedächtnis, der sich nur auf seinen aktuellen Zustand stützt, um seinen zukünftigen Zustand zu bestimmen.

Eine Markov-Kette wird durch eine Menge von Zuständen und die Wahrscheinlichkeiten, von einem Zustand in einen anderen zu gelangen, definiert.

Diese Wahrscheinlichkeiten werden oft in einer Übergangsmatrix dargestellt, wobei jedes Element der Matrix die Wahrscheinlichkeit darstellt, von einem Zustand in einen anderen überzugehen.

Die Markov-Kette ist im Bereich Trading/Investment wichtig, da sie zur Modellierung des Verhaltens von Finanzmärkten verwendet werden kann.

Der Aktienmarkt ist beispielsweise ein komplexes System mit einer Vielzahl von Variablen, die sich auf den Preis der Wertpapiere auswirken, aus denen er besteht.

Die Markov-Kette ermöglicht eine Vereinfachung des Systems, indem sie sich nur auf den aktuellen Zustand des Marktes und die Wahrscheinlichkeiten für den Übergang in andere Zustände konzentriert.

Indem man den Aktienmarkt als Markov-Kette modelliert, können Händler und Investoren potenziell eine zusätzliche Perspektive gewinnen, indem sie zukünftige Marktbewegungen auf der Grundlage des aktuellen Marktzustands vorhersagen.

Die Markov-Kette kann auch als Hilfe bei der Berechnung verschiedener Kennzahlen wie erwartete Renditen, Volatilität und Risiko verwendet werden.

Darüber hinaus wird die Markov-Kette in verschiedenen Techniken der Finanzmodellierung eingesetzt, z. B. bei der Bewertung von Optionen, der Portfoliooptimierung und dem Risikomanagement.

Sie ermöglicht es Händlern/Investoren, verschiedene Anlagestrategien zu entwickeln und zu testen und die Wirksamkeit dieser Strategien unter verschiedenen Marktbedingungen zu messen.

Zufälliges Gehen

Der Zufallsmarsch ist ein mathematisches Konzept aus der Wahrscheinlichkeitstheorie, das die Bewegung eines Objekts auf zufällige und unvorhersehbare Weise beschreibt.

Bei einem Random Walk wird die nächste Position des Objekts durch einen Zufallsprozess bestimmt, z. B. durch das Ziehen eines Loses oder das Werfen eines Würfels.

Im Finanzwesen wird ein Random-Walk-Modell häufig verwendet, um die Entwicklung von Aktienkursen im Laufe der Zeit zu beschreiben.

Die Theorie, die diesem Modell zugrunde liegt, ist, dass die Bewegung der Aktienkurse unvorhersehbar ist und einem Zufallsmuster folgt.

Das bedeutet, dass der Kurs einer Aktie zu einem bestimmten Zeitpunkt mit gleicher Wahrscheinlichkeit steigt wie fällt und dass die Entwicklung des Aktienkurses im Laufe der Zeit nicht von vergangenen Kursen oder anderen externen Faktoren beeinflusst wird. (Natürlich gibt es verschiedene Ideen und Theorien zu Trends, Momentum usw.).

Das Konzept des Random Walk ist im Bereich des Handels und der Investition nützlich zu kennen, da es darauf hindeutet, dass es sehr schwierig ist, die Entwicklung von Aktienkursen vorherzusagen.

Das bedeutet, dass es schwierig ist, den Markt ständig zu schlagen, indem man Aktien auf der Grundlage vergangener Kursbewegungen oder anderer Informationen kauft und verkauft.

Anleger und Händler können das Konzept des Random Walk nutzen, um ihre Anlagestrategie zu untermauern und fundiertere Entscheidungen zu treffen.

Beispielsweise können sie sich dafür entscheiden, in ein diversifiziertes Aktienportfolio zu investieren, um ihre Anfälligkeit für einzelne Kursbewegungen an der Börse zu verringern und nach Vermögenswerten, Anlageklassen, Ländern und Währungen zu diversifizieren, und sie können den Einsatz einer Buy-and-Hold-Strategie in Betracht ziehen, um die Kosten und Risiken häufiger Transaktionen zu vermeiden.

Stochastischer Prozess

Der stochastische Prozess ist ein mathematischer Rahmen, der zur Modellierung des Verhaltens eines Systems verwendet wird, das sich im Laufe der Zeit zufällig entwickelt.

Es handelt sich um eine Sammlung von zeitindizierten Zufallsvariablen, d. h. der Wert des Prozesses zu einem bestimmten Zeitpunkt ist zufällig.

Stochastische Prozesse sind in der Wahrscheinlichkeitstheorie nützlich, weil sie uns helfen können, das Verhalten von zufälligen Phänomenen, die sich im Laufe der Zeit verändern, zu analysieren.

Sie bieten eine Möglichkeit, die Zufälligkeit dieser Phänomene zu modellieren und zu verstehen, die dazu verwendet werden kann, Vorhersagen zu treffen und Entscheidungen auf der Grundlage erwarteter Ergebnisse zu treffen.

Im Bereich des Handels und der Investitionen werden stochastische Prozesse verwendet, um bestimmte Verhaltensweisen der Finanzmärkte und der Preise von Vermögenswerten zu modellieren.

Sie ermöglichen die Analyse der Zufälligkeit und der Volatilität von Finanzdaten, die für Entscheidungen über den Zeitpunkt des Kaufs oder Verkaufs von Vermögenswerten genutzt werden können.

Stochastische Prozesse können beispielsweise verwendet werden, um die Bewegung von Aktienkursen oder Wechselkursen zu modellieren, was Händlern und Anlegern dabei helfen kann, Vorhersagen über zukünftige Bewegungen dieser Märkte zu treffen.

Stochastische Prozesse werden auch zur Entwicklung und zum Testen von Handelsstrategien verwendet. Indem sie das Verhalten der Finanzmärkte mithilfe stochastischer Prozesse simulieren, können Händler und Investoren ihre Handelsstrategien testen und ihre Leistung unter verschiedenen Marktbedingungen bewerten.

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie, das sich auf die Wahrscheinlichkeit bezieht, dass ein Ereignis eintritt, wenn ein anderes Ereignis bereits eingetreten ist. Sie ist eine Möglichkeit, unsere Wahrscheinlichkeitsschätzungen auf der Grundlage neuer Informationen zu aktualisieren.

Formaler ausgedrückt wird die bedingte Wahrscheinlichkeit eines Ereignisses A, da das Ereignis B eingetreten ist, wie folgt definiert:

P(A | B) = P(A und B) / P(B).

Wobei:

• P(A und B) ist die Wahrscheinlichkeit, dass die beiden Ereignisse A und B eintreten, und
• P(B) ist die Wahrscheinlichkeit, dass das Ereignis B eintritt.

Die bedingte Wahrscheinlichkeit ist beim Trading und Investieren wichtig, weil sie uns ermöglicht, unsere Wahrscheinlichkeitsschätzungen zu aktualisieren, wenn neue Informationen verfügbar werden.

Wenn wir zum Beispiel wissen, dass ein Unternehmen gerade einen positiven Gewinnbericht angekündigt hat, ist die bedingte Wahrscheinlichkeit, dass der Aktienkurs unter Berücksichtigung dieser Information steigt, höher als vor der Ankündigung.

Anleger und Händler nutzen die bedingte Wahrscheinlichkeit, um auf der Grundlage neuer Informationen besser informierte Entscheidungen zu treffen.

Indem sie ihre Wahrscheinlichkeitsschätzungen aktualisieren, können sie die potenziellen Risiken und Gewinne einer bestimmten Investition besser einschätzen.

Dies kann ihnen helfen, profitablere Geschäfte zu tätigen und ihre Risiken effektiver zu steuern.

Nehmen wir zum Beispiel an, dass ein Anleger den Kauf einer Aktie in Erwägung zieht, die schon immer volatil war.

Mithilfe der bedingten Wahrscheinlichkeit kann der Anleger die Wahrscheinlichkeit einschätzen, dass der Kurs der Aktie aufgrund verschiedener Marktbedingungen, wie z. B. Änderungen der Zinssätze, des Wachstums, der Inflation, der Politik oder geopolitischer Ereignisse, steigt oder fällt.

Diese Informationen können dem Anleger helfen, eine fundiertere Entscheidung über den Kauf, das Halten oder den Verkauf der Aktie zu treffen.

Gesetz der großen Zahlen

Das Gesetz der großen Zahlen ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie, das das Verhalten des Mittelwerts einer großen Anzahl von unabhängigen Zufallsvariablen beschreibt.

Dieses Gesetz besagt, dass mit zunehmender Anzahl unabhängiger Versuche der Mittelwert dieser Versuche gegen den Erwartungswert der zugrunde liegenden Wahrscheinlichkeitsverteilung konvergiert.

Einfacher ausgedrückt besagt das Gesetz der großen Zahlen, dass die beobachteten Ergebnisse umso näher am erwarteten Ergebnis liegen, je öfter ein Experiment wiederholt wird.

Beispiel: Eine Münze wird geworfen.

Wird beispielsweise mehrmals eine Münze geworfen, sagt das Gesetz der großen Zahlen voraus, dass sich die Häufigkeit der Köpfe mit zunehmender Anzahl der Würfe der 50 %-Marke annähert.

Bei 1 000 Versuchen ist es extrem unwahrscheinlich, dass eine faire Münze 55/45 in die eine oder andere Richtung erzielt (0,17 %), aber bei 100 Würfen ist dies durchaus möglich (36,8 %).

Warum ist es nützlich?

Das Gesetz der großen Zahlen ist beim Handeln und Investieren nützlich, weil es das Risiko unvorhersehbarer Marktschwankungen mindert.

Durch Investitionen in ein diversifiziertes Portfolio kann ein Anleger sein Risiko auf eine große Anzahl von Vermögenswerten verteilen, was dazu beitragen kann, die Auswirkungen der Preisbewegungen einzelner Vermögenswerte zu verringern.

Darüber hinaus ist das Gesetz der großen Zahlen nützlich, um historische Marktdaten zu analysieren und so fundierte Investitionsentscheidungen zu treffen.

Durch die Untersuchung einer großen Anzahl historischer Markttrends können Investoren helfen, Muster und Trends zu erkennen, die ihnen helfen können, fundiertere Anlageentscheidungen zu treffen.

Wenn ein Händler beispielsweise wissen möchte, ob die Federal Reserve trotz einer über ihrem Ziel liegenden Inflation die Zinsen bereits gesenkt hat, kann er in der Geschichte nachsehen, ob es Präzedenzfälle gibt und wie sich dies auf verschiedene Anlagemärkte ausgewirkt hat.

Wenn es eine Stichprobe gibt, wie groß ist sie, um genügend nützliche Daten zu erhalten, um sinnvolle Schlussfolgerungen zu ziehen?

Wie hängt das Gesetz der großen Zahlen mit der statistischen Signifikanz zusammen?

Das Gesetz der großen Zahlen und die statistische Signifikanz sind verwandte Konzepte in der Statistik, aber sie sind nicht identisch.

Das Gesetz der großen Zahlen bezieht sich auf die Tatsache, dass der Stichprobenmittelwert einer großen Anzahl unabhängiger Beobachtungen gegen den Erwartungswert der zugrunde liegenden Wahrscheinlichkeitsverteilung konvergiert, wenn die Anzahl der Beobachtungen gegen unendlich geht.

Die statistische Signifikanz hingegen ist ein Maß für die Wahrscheinlichkeit, dass die beobachteten Ergebnisse einer Studie nicht auf Zufall beruhen.

Bei statistischen Hypothesentests gilt ein Ergebnis als statistisch signifikant, wenn die Wahrscheinlichkeit, das beobachtete Ergebnis zufällig zu erhalten, unter einem vordefinierten Schwellenwert liegt, in der Regel 5 % oder weniger.

In der Praxis kann das Gesetz der großen Zahlen zur Untermauerung der statistischen Signifikanz herangezogen werden.

Wenn eine große Stichprobe erhoben wird und der Stichprobenmittelwert nahe am Erwartungswert der zugrunde liegenden Verteilung liegt, deutet dies darauf hin, dass die beobachteten Ergebnisse weniger wahrscheinlich zufällig sind und mit größerer Wahrscheinlichkeit statistisch signifikant sind.

Es ist jedoch wichtig zu beachten, dass statistische Signifikanz nicht notwendigerweise praktische Bedeutung oder wirtschaftliche Relevanz impliziert und dass statistische Signifikanz allein nicht verwendet werden sollte, um wichtige Entscheidungen zu treffen.

Um fundierte Entscheidungen treffen zu können, ist es unerlässlich, die zugrunde liegenden Daten, die statistischen Methoden und den Kontext des untersuchten Problems zu verstehen.

Bayes'sches Theorem

Das Bayes-Theorem ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie, das beschreibt, wie Wahrscheinlichkeiten aufgrund neuer Beweise oder Informationen aktualisiert werden können.

Es wurde nach Reverend Thomas Bayes benannt, einem britischen Statistiker und Theologen des 18. Jahrhunderts.

Das Theorem bietet eine Möglichkeit, die Wahrscheinlichkeit einer Hypothese oder eines Ereignisses auf der Grundlage von früherem Wissen oder Überzeugungen (als frühere Wahrscheinlichkeit bezeichnet) und neuen Beweisen (als Wahrscheinlichkeit bezeichnet) zu berechnen.

Die aktualisierte Wahrscheinlichkeit wird als posteriore Wahrscheinlichkeit bezeichnet und stellt die Wahrscheinlichkeit der Hypothese oder des Ereignisses nach Berücksichtigung der neuen Beweise dar.

Die Formel für das Bayes'sche Theorem lautet wie folgt:

P(A|B) = P(B|A) * P(A) / P(B).

Wobei:

• P(A|B) ist die spätere Wahrscheinlichkeit des Ereignisses A unter der Voraussetzung des Beweises B.
• P(B|A) ist die Wahrscheinlichkeit des Beweises B angesichts des Ereignisses A.
• P(A) ist die frühere Wahrscheinlichkeit des Ereignisses A und
• P(B) ist die Wahrscheinlichkeit des Beweises B.

Das Bayes'sche Theorem ist im Bereich des Handels und der Investition nützlich, da es Anlegern helfen kann, ihre Überzeugungen über die Wahrscheinlichkeit verschiedener Ereignisse auf der Grundlage neuer Informationen, wie z. B. Nachrichten über Unternehmensgewinne oder Wirtschaftsindikatoren, zu aktualisieren.

Und das ist ein wesentlicher Aspekt der Bayes'schen Wahrscheinlichkeitstheorie: Sie aktualisiert Ihre vorherigen Überzeugungen, ohne sie notwendigerweise zu bestimmen oder von Grund auf neu zu berechnen.

Durch die Anwendung des Bayes'schen Theorems können Anleger ihre Wahrscheinlichkeiten aktualisieren und fundiertere Anlageentscheidungen treffen.

Beispiele dafür, wie wichtig es ist, unsere Annahmen zu überprüfen.

Schalterbeamter in einer Bank

Ein berühmtes Beispiel für das Bayes'sche Theorem in Aktion stammt aus der Studie von Kahneman und Tversky.

In dieser Studie erhielten die Teilnehmer folgende Informationen:

Linda ist 31 Jahre alt, ledig, hat eine klare Meinung und ist sehr intelligent. Sie hat Philosophie studiert. Als Studentin beschäftigte sie sich intensiv mit Fragen der Diskriminierung und der sozialen Gerechtigkeit und nahm auch an Anti-Atomkraft-Demonstrationen teil.

Die Teilnehmer wurden dann gebeten, die Wahrscheinlichkeit von zwei möglichen Szenarien zu bewerten:

• Linda ist Bankkassiererin.
• Linda ist Bankkassiererin und in der feministischen Bewegung aktiv.

Trotz der Tatsache, dass das erste Szenario mehr Personen umfasst (alle Kassierer) als das zweite (Kassierer und Feministin), stuften viele Teilnehmer das zweite Szenario als wahrscheinlicher ein.

Dies lag daran, dass Lindas Beschreibung ihrem Stereotyp einer Feministin entsprach, obwohl die Wahrscheinlichkeit, dass beide Ereignisse eintreten, geringer ist als die Wahrscheinlichkeit des ersten Ereignisses.

Dieses Beispiel zeigt, wie wichtig es ist, unsere Annahmen zu überprüfen und alle verfügbaren Informationen zu berücksichtigen, bevor wir eine Entscheidung treffen.

Das Bayes'sche Theorem kann Anlegern helfen, ihre Wahrscheinlichkeiten zu aktualisieren und Verzerrungen zu vermeiden, die zu falschen Entscheidungen führen können.

Ist Steve Bauer oder Bibliothekar?

Die berühmte Studie von Kahneman und Tversky beinhaltete ein weiteres Szenario, in dem die Teilnehmer auf der Grundlage begrenzter Informationen über seine Persönlichkeit die Wahrscheinlichkeit bestimmen mussten, dass Steve entweder ein Bauer oder ein Bibliothekar ist.

Die Teilnehmer erhielten folgende Informationen:

Steve ist ein ruhiger, schüchterner Mensch, der gerne Bücher liest und nicht sehr gesellig ist.

Allein aufgrund dieser Informationen kamen die meisten Teilnehmer zu dem Schluss, dass Steve eher ein Bibliothekar als ein Bauer ist. Kahneman und Tversky zeigten jedoch, dass diese Schlussfolgerung nicht unbedingt gerechtfertigt war.

Um dies zu demonstrieren, präsentierten sie den Teilnehmern zusätzliche Informationen, die relevant, aber nicht in der ursprünglichen Beschreibung enthalten waren.

Beispielsweise fügten sie Informationen über die Anzahl der Landwirte im Vergleich zu Bibliothekaren und den Prozentsatz der Landwirte mit Steves Persönlichkeitstyp hinzu, was immer noch eine höhere Zahl von Landwirten als die Gesamtzahl von Bibliothekaren ergab.

Wenn es beispielsweise 20-mal mehr Landwirte als Bibliothekare gibt und 20 % der Landwirte zu diesem Persönlichkeitstyp passen, ist es immer noch 4-mal (20 * 0,20) wahrscheinlicher, dass Steve ein Landwirt als ein Bibliothekar ist.

Als die Teilnehmer diese neuen Informationen erhielten, stieg ihre Wahrscheinlichkeit, dass Steve ein Bauer war, erheblich an, was darauf hinweist, dass ihre anfänglichen Schlussfolgerungen nicht ausreichend informiert waren.

Diese Studie unterstreicht, wie wichtig es ist, Annahmen zu testen, wenn Entscheidungen auf der Grundlage begrenzter Informationen getroffen werden.

Es ist wichtig, alle relevanten Faktoren zu berücksichtigen und sich bei Entscheidungen oder Urteilsbildungen nicht nur auf anfängliche Annahmen oder Heuristiken wie Stereotype zu verlassen.

Dieser Ansatz steht im Einklang mit dem Bayes'schen Wahrscheinlichkeitsansatz, der die kontinuierliche Aktualisierung von Überzeugungen auf der Grundlage neuer Informationen beinhaltet.

Beim Handeln und Investieren ist es immer wichtig zu fragen, woher weißt du, dass du es weißt?

Korrelation und Kovarianz

Korrelation und Kovarianz sind zwei statistische Begriffe, die in der Wahrscheinlichkeitstheorie häufig verwendet werden, um die Beziehung zwischen zwei Zufallsvariablen zu beschreiben.

Die Kovarianz misst, inwieweit sich zwei Zufallsvariablen gemeinsam bewegen, während die Korrelation die Stärke und Richtung ihrer Beziehung misst.

Eine positive Kovarianz zeigt an, dass sich die beiden Variablen tendenziell in die gleiche Richtung bewegen, während eine negative Kovarianz anzeigt, dass sie sich tendenziell in entgegengesetzte Richtungen bewegen.

Ein Korrelationskoeffizient reicht von -1 bis 1, wobei Werte von 1 auf eine perfekte positive Korrelation hinweisen, Werte von -1 auf eine perfekte negative Korrelation und Werte von 0 auf keine Korrelation.

Im Bereich Trading/Investment sind Korrelation und Kovarianz nützliche Instrumente für das Risikomanagement und die Diversifizierung des Portfolios.

Wenn Anleger die Beziehung zwischen verschiedenen Vermögenswerten verstehen, können sie ihre Portfolios besser verwalten, indem sie Vermögenswerte auswählen, die nicht stark miteinander korrelieren.

Dies kann dazu beitragen, das Gesamtrisiko des Portfolios zu verringern, indem die Investitionen auf verschiedene Anlageklassen und Sektoren verteilt werden.

Beispielsweise kann ein Portfolio aus Aktien mit hoher Korrelation untereinander riskanter sein als ein Portfolio aus Aktien oder anderen Vermögenswerten mit geringer Korrelation untereinander.

Durch die Auswahl einer diversifizierten Palette von Vermögenswerten mit geringer Korrelation kann ein Anleger ein widerstandsfähigeres Portfolio zusammenstellen, das im Falle eines Marktabschwungs weniger wahrscheinlich große Verluste erleidet.

Darüber hinaus kann das Verständnis von Korrelation und Kovarianz Anlegern helfen, Muster auf dem Markt zu erkennen und zukünftige Trends vorherzusagen.

Es ist auch wichtig zu verstehen, dass Korrelationen rückwärts gerichtet sind und sich tendenziell im Laufe der Zeit verändern.

Beispielsweise können Aktien und Anleihen in einem Umfeld, in dem die Veränderungen der diskontierten Inflation zurückgehen, negativ korreliert sein, während sie in Umgebungen, in denen die diskontierte Inflation steigt, positiv korreliert sein können.

Somit werden robustere Interpretationen der Inflation den intrinsischen Zustand von Vermögenswerten auf der Grundlage wirtschaftlicher Ursache-Wirkungs-Zusammenhänge genauer untersuchen als retrospektive Interpretationen wie einfache Korrelationskoeffizienten, die nur ein flüchtiges Nebenprodukt des Umfelds sind, in dem sie sich befinden.

CFD-Broker

CFD Brokers	Plattform	Reguliert durch die	Eröffnen Sie ein Demokonto
	MetaTrader 4 und 5 AvaOptions	ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM
	MetaTrader 4 und 5  cTrader, TradingView	FCA, ASIC, CySEC, BaFin, DFSA, SCB, CMA
	xStation 5	FCA, KNF, CySEC, BIFSC, CNMV, DFSA
	MetaTrader 4 und 5	CySEC, FCA, ASIC, JSC, OCRCVM, FSCA
	MetaTrader 4 und 5 ActivTrader, TradingView	FCA, CSSF, SCB, BACEN & CVM, CMVM
	IG, ProRealTime, MT4, L2 Dealer	FCA, BaFin, ASIC, FINMA, FSCA, MAS, FMA, DFSA, JFSA, CFTC
	MetaTrader 4 und 5	CySEC, ASIC, BIFSC
ASIC: Australien, BaFin: Deutschland, BIFSC: Belize, BVI FSC: Britische Jungferninseln, BACEN & CVM : Brasilien, CySEC: Zypern, CNMV: Spanien, CMVM : Portugal, CSSF: Luxemburg, CFTC: USA, CBFSAI: Irland, CMA: Oman,, DFSA: Dubai, FCA: Großbritannien, FINMA: Schweiz, FSPR - FMA: Neuseeland, FRSA: Abu Dhabi, FSA: Seychellen, FSCA: Südafrika, JFSA: Japan, JSC: Jordanien, KNF: Polen, MAS: Singapur, OCRCVM: Kanada, SCB: Bahamas, VFSC: Vanuatu.
Der CFD-Handel birgt ein erhebliches Verlustrisiko, weshalb er nicht für alle Anleger geeignet ist. 74-89 % der Kleinanlegerkonten verlieren beim Handel mit CFDs Geld.

FAQs - Wahrscheinlichkeitstheorie beim Trading

Schlussfolgerung - Die Wahrscheinlichkeitstheorie im Trading

Die Wahrscheinlichkeitstheorie spielt beim Trading eine entscheidende Rolle, da sie den Tradern hilft, fundierte Entscheidungen auf der Grundlage einer datengestützten Analyse zu treffen.

Mithilfe der Wahrscheinlichkeitstheorie können Trader die Wahrscheinlichkeit potenzieller Marktbewegungen einschätzen und Handelsstrategien entwickeln, um aus diesen Bewegungen Kapital zu schlagen.

Sie hilft Händlern, das Risiko-Ertrags-Verhältnis einer Transaktion zu bewerten, ihr Portfolio zu verwalten und ihre Positionen zu optimieren.

Die Wahrscheinlichkeitstheorie ist besonders nützlich, um die Unsicherheit zu quantifizieren und die Marktvolatilität zu messen, sodass Händler Marktveränderungen vorhersehen und sich darauf vorbereiten können.

Insgesamt gibt die Wahrscheinlichkeitstheorie den Händlern die notwendigen Werkzeuge an die Hand, um informiertere und präzisere Handelsentscheidungen zu treffen, was zu einer höheren Rentabilität und einem geringeren Risiko führen kann.