نظرية الاحتمالات والتداول
ما هي نظرية الاحتمالات ولماذا هي مهمة؟

نظرية الاحتمالية ضرورية في التداول والاستثمار لأنها تسمح للمشاركين في السوق بفهم وقياس عدم اليقين والمخاطر المرتبطة بالقرارات المالية.
مثل الحياة نفسها ، فإن التجارة تدور حول الاحتمالات. نادرًا ما توجد نتائج واضحة بالأبيض والأسود يسهل الاستفادة منها.
باستخدام نظرية الاحتمالات ، يمكن للمتداولين / المستثمرين اتخاذ قرارات أكثر استنارة بناءً على احتمالية النتائج المختلفة.
فيما يلي بعض الأسباب التي تجعل نظرية الاحتمالات مهمة جدًا في التداول / الاستثمار:
حدد المخاطر
تسمح نظرية الاحتمالات للمستثمرين بحساب احتمالية حدوث أشياء مختلفة ، بما في ذلك السيناريوهات الإيجابية والسلبية.
يتيح ذلك للمتداولين فهم المخاطر المحتملة المرتبطة بالتداولات / الاستثمارات المختلفة بشكل أفضل.
صناعة القرار
تسمح نظرية الاحتمالات للمتداولين باتخاذ قرارات أفضل بناءً على احتمالية حدوث نتائج مختلفة وتقييم الاحتمالات بأنفسهم (ما يمكن أن يسمى "احتمالات الاحتمالات" ، لأن احتمالات حدوث أشياء مختلفة غير معروفة بأنفسهم).
على سبيل المثال ، إذا كان الاستثمار أو التجارة لديه احتمال 70٪ لتحقيق عائد إيجابي على مدار عام واحد ، فكيف تعرف؟
تغطي نظرية الاحتمالات أشياء مثل التباين وكيفية التعامل بشكل أفضل مع ما لا تعرفه ولا تعرفه.
إدارة المحافظ
تساعد نظرية الاحتمالات المتداولين / المستثمرين على إدارة محافظهم من خلال توفير طريقة لتقييم المخاطر المرتبطة بفئات الأصول المختلفة.
من خلال تحليل احتمالية النتائج المختلفة ، يمكن للمتداولين / المستثمرين إنشاء محفظة متنوعة توازن بين المخاطر والعائد.
إدارة المخاطر
تعتبر نظرية الاحتمالية مهمة أيضًا في إدارة المخاطر ، لأنها تساعد المستثمرين على تحديد احتمالية الأحداث التي قد تؤثر سلبًا على استثماراتهم / عملياتهم واتخاذ خطوات للتخفيف منها.
بشكل عام ، تعتبر نظرية الاحتمالات أداة مهمة تسمح للمستثمرين / المتداولين بفهم المخاطر والعوائد المحتملة لفرص الاستثمار المختلفة ، لاتخاذ خيارات أكثر استنارة وتحقيق نتائج أفضل على المدى الطويل.
في هذه المقالة سوف ندرس الفروع المختلفة لنظرية الاحتمالات وتطبيقاتها في مجال التداول.
فرصة
في نظرية الاحتمالات ، تشير العشوائية إلى حقيقة أن نتيجة حدث ما لا يمكن التنبؤ بها وقد تختلف من تجربة إلى أخرى.
غالبًا ما يتم نمذجة هذه الظاهرة باستخدام التوزيعات الاحتمالية ، التي تصف احتمالية كل نتيجة محتملة.
العشوائية هي مفهوم أساسي في نظرية الاحتمالات لأنها تسمح لنا بتحديد المجهول وإجراء تنبؤات حول المستقبل من معلومات غير كاملة.
في العديد من مواقف العالم الحقيقي ، تتأثر نتائج الأحداث بعدد كبير من المتغيرات التي يصعب ، إن لم يكن من المستحيل ، التنبؤ بها بدقة / يقينًا.
تسمح العشوائية بأخذ ذلك في الاعتبار وإمكانية تقدير النتائج المختلفة بناءً على البيانات التاريخية أو السبب الاقتصادي والنتيجة أو معلومات أخرى.
في مجال التجارة والاستثمار ، الفرصة موجودة دائمًا لأن الأسواق المالية تخضع لمجموعة واسعة من التأثيرات.
هناك أنواع مختلفة من الأشخاص في الأسواق ، بأحجام مختلفة ، ولديهم دوافع مختلفة للتداول.
يمكن أن تتجلى العشوائية في شكل تقلبات في السوق أو أحداث غير متوقعة أو عوامل أخرى يمكن أن تسبب تقلبات سريعة وغير متوقعة في الأسعار.
يعد فهم هذه العشوائية واستيعابها أمرًا أساسيًا لتطوير استراتيجيات تداول ناجحة وإدارة المخاطر.
كلما زادت خبرة الأشخاص في الأسواق ، زاد إدراكهم أن كل ما يعرفونه ضعيف مقارنة بالأشياء التي يجب معرفتها بناءً على ما يتم خصمه في الأسواق.
إحدى الطرق التي يمكن للمتداولين والمستثمرين من خلالها التعامل مع العشوائية هي استخدام النماذج القائمة على الاحتمالات لاتخاذ القرارات.
على سبيل المثال ، يمكن للمتداول استخدام نموذج إحصائي لتقدير احتمال ارتفاع أو انخفاض سعر أصل معين خلال فترة معينة. يمكن بعد ذلك استخدام هذه المعلومات لبناء محفظة متوازنة وإدارة المخاطر.
على سبيل المثال ، إذا كان توزيع السعر المخفض لأصل معين يبدو كالتالي:
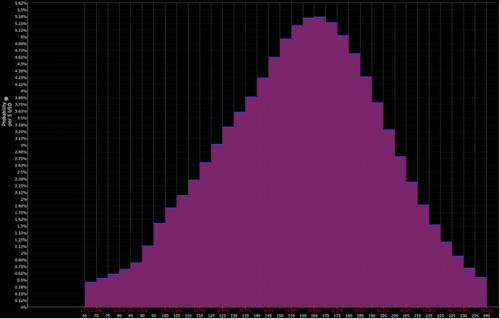
ويكون تفسير المتداول أقرب إلى الجمع بين التوزيعين الأحمر والأرجواني (أي الميل الهبوطي):
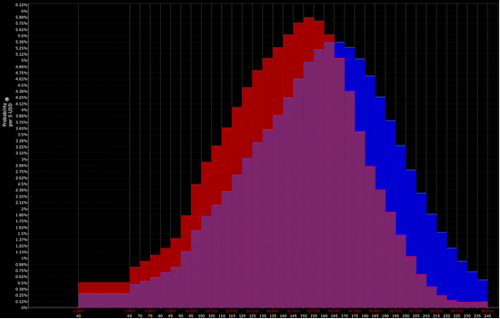
يمكنهم بعد ذلك توقع اتخاذ موقف هبوطي على الأصل. ثم ، بالطبع ، هناك مسألة كيفية وضعها في مكانها وحجمها.
التفرد المتبادل
في نظرية الاحتمالات ، يشير مفهوم الحصرية المتبادلة إلى ملكية حدثين مختلفين عن بعضهما البعض.
رياضياً ، يقال إن حدثين A و B متنافيان إذا كان تقاطعهما (أي الحدث الذي يحدث فيه كل من A و B) فارغًا ، أي P (A ∩ B) = 0.
يعد التفرد المتبادل أمرًا مهمًا في التداول / الاستثمار لأنه يساعد المستثمرين على فهم كيفية إدارة مخاطرهم بشكل أفضل.
عندما يحتفظ المستثمرون بمحفظة أصول ، فإنهم بحاجة إلى النظر في العلاقات المتبادلة بين أصولهم.
على سبيل المثال ، افترض أن متداولًا / مستثمرًا يمتلك محفظة أسهم تتضمن شركات التكنولوجيا وشركات النفط. إذا ارتفع سعر النفط ، فقد يساعد ذلك شركات النفط ولكن مخزونات التكنولوجيا قد تتضرر (على سبيل المثال ، بسبب التأثير السلبي لارتفاع أسعار النفط على أسعار الفائدة) ، والعكس صحيح.
ومع ذلك ، إذا حدثت تطورات معينة في كل قطاع ، فقد لا تؤثر على أسعار الأوراق المالية في القطاع الآخر.
لذلك ، في حين أن الأوراق المالية مرتبطة ببعضها البعض في بعض النواحي - مثل التغييرات في النمو المخصوم والتضخم - فإنهما يستبعدان بعضهما البعض بطرق أخرى.
كيف يتم فصل هذه العوامل المتنافية؟
في بعض الأحيان تكون طبيعة التدفق المالي فقط - على سبيل المثال ، النفط مقابل المنتجات / الخدمات التقنية.
في بعض الأحيان يطلق عليها عوامل - على سبيل المثال ، الزخم والحجم والجودة والقيمة ، إلخ.
أيضًا ، يعد التفرد المتبادل أمرًا مهمًا في تداول الخيارات ، حيث يمكن أن يعتمد العائد على الخيار في كثير من الأحيان على عدم حدوث حدث آخر. في هذا السياق ، يساعد التفرد المتبادل المشغلين على التحوط من مخاطرهم وإدارة تعرضهم.
تجربة (اختبار برنولي)
تعتبر تجربة أو تجربة برنولي مفهومًا أساسيًا في نظرية الاحتمالية التي تشير إلى حدث عشوائي له نتيجتان محتملتان فقط.
على سبيل المثال ، رمي العملة هو تجربة برنولي ، حيث تكون النتائج المحتملة هي الرؤوس أو الذيل.
مثال آخر هو ما إذا كانت تجارة خيار معين ستدفع (في المال) أم لا (خارج نطاق المال) عند انتهاء الصلاحية.
في نظرية الاحتمالات ، يتم تحديد احتمال النجاح (أي النتيجة التي نهتم بها) بواسطة p ، واحتمال الفشل (أي النتيجة الأخرى) بواسطة q = 1 - p.
غالبًا ما يتم تعيين نتائج تجربة برنولي على أنها 1 للنجاح و 0 للفشل.
تكمن أهمية مقالات برنولي في مجال التجارة والاستثمار في أن بعض القرارات المالية تنطوي على نتائج ثنائية.
على سبيل المثال ، قد تقرر شراء خيار سهم على أمل أن ينكسر ، أو يمكنك اختيار بيعه على أمل أن ينخفض سعره وستحصل على قسط التأمين الكامل.
في كلتا الحالتين ، تكون النتيجة ثنائية من حيث المال. الرهانات الثنائية النقية تأتي في شكل خيارات ثنائية.
من خلال تطبيق مبادئ نظرية الاحتمالات على التداول والاستثمار ، يمكنك اتخاذ قرارات مستنيرة بشأن وقت الشراء أو البيع.
هناك أيضًا مفاهيم مثل القيمة المتوقعة ، والتي تعلمك ألا تراهن دائمًا على النتيجة الأكثر احتمالية.
توزيع الاحتمالات
في نظرية الاحتمالات ، توزيع الاحتمالات هو دالة تصف احتمالية النتائج المختلفة في تجربة أو عملية عشوائية.
يحدد احتمالات جميع النتائج المحتملة لحدث ما ، ومجموع احتمالات جميع النتائج يساوي واحدًا.
هناك العديد من أنواع التوزيعات الاحتمالية ، ولكن أكثرها شيوعًا تشمل التوزيع الطبيعي والتوزيع ذي الحدين وتوزيع بواسون.
لكل توزيع مجموعة خاصة به من المعلمات التي تحدد شكله ، وغالبًا ما تُستخدم هذه المعلمات لعمل تنبؤات واتخاذ القرارات.
بالطبع ، في الأسواق المالية ، تميل العوائد إلى أن تكون ذات ذيول أكبر ولا تتناسب مع توزيع محدد مسبقًا ، لذلك تميل إلى أن تكون مخصصة.
بشكل عام ، التوزيعات الاحتمالية مهمة لأنها توفر إطارًا لفهم المخاطر وعدم اليقين المرتبطين بالاستثمارات المالية.
أحد أهم المفاهيم في التداول / الاستثمار هو أن كل شيء هو احتمال (أي توزيع النتائج المحتملة). لا توجد نتيجة واحدة محتملة بشكل خاص.
باستخدام التوزيعات الاحتمالية ، يمكن للمتداولين والمستثمرين تقدير احتمالية النتائج المختلفة واتخاذ قرارات أكثر استنارة حول كيفية تخصيص مواردهم.
على سبيل المثال ، يمكن للمتداول استخدام التوزيع العادي أو التوزيع ذي الطرف الأكبر لنمذجة العوائد اليومية لسهم معين.
يمكنه بعد ذلك استخدام هذا التوزيع لتقدير احتمالية أن يتجاوز عائد السهم حدًا معينًا ، مثل عائد +/- 5٪ في يوم واحد.
باستخدام التوزيعات الاحتمالية بهذه الطريقة ، يمكن للمتداولين إدارة مخاطرهم بشكل أفضل وتحسين عوائدهم.
إلى جانب تقدير الاحتمالات ، تُستخدم التوزيعات الاحتمالية أيضًا لإنشاء أدوات مالية مثل الخيارات والعقود الآجلة.
يتم تسعير هذه الأدوات بناءً على التوزيع الأساسي للأصل المرتبط بها ، ويمكن للمتداولين استخدامها للتحوط من مخاطرهم أو المراهنة على تحركات الأسعار المستقبلية للأصل.
بالإضافة إلى ذلك ، يمكن إنشاء التوزيعات بناءً على سعر الخيارات الأساسية ، كما هو موضح أدناه.
التوزيع حسب تحديث الأسواق:
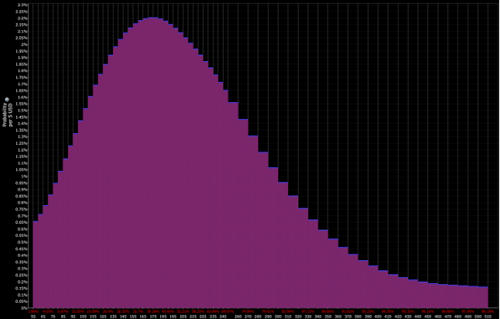
التوزيع الذي يحدده المتداول (والذي يفتح الباب أمام الفرص التكتيكية):
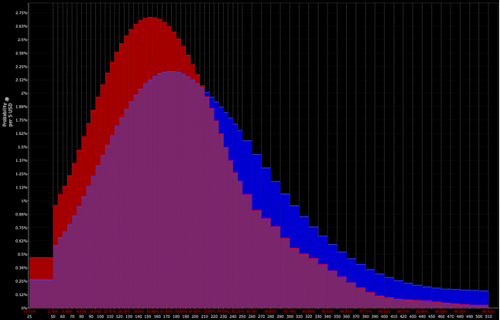
توزيع ثنائي
التوزيع ذو الحدين هو توزيع احتمالي يمثل عدد النتائج الإيجابية في سلسلة من التجارب المستقلة المتطابقة ، حيث يكون لكل تجربة نتيجتان محتملتان فقط (على سبيل المثال ، الرؤوس أو الذيل ، الفوز أو الخسارة ، عالية أو منخفضة).
المعلمات الرئيسية للتوزيع ذي الحدين هي احتمال نجاح تجربة واحدة (يُشار إليها بالرمز p) وعدد المحاولات (يُشار إليها بالرمز n).
التوزيع ذو الحدين مهم في مجال التداول والاستثمار لأنه يمكن استخدامه لنمذجة توزيع العوائد من استراتيجية تداول ثنائية (على سبيل المثال ، استراتيجية تتضمن شراء أو بيع أصل اعتمادًا على ما إذا كان حدث معين أو حدث لا).
على وجه الخصوص ، يمكن حساب القيمة المتوقعة لإستراتيجية تداول ثنائي باستخدام التوزيع ذي الحدين.
القيمة المتوقعة لإستراتيجية تداول ثنائي هي مجموع منتجات احتمالية كل نتيجة محتملة والعائد المقابل لتلك النتيجة.
على سبيل المثال ، إذا كانت استراتيجية التداول الثنائي لديها احتمال 60٪ لتحقيق عائد بنسبة 10٪ واحتمال 40٪ لتحقيق عائد بنسبة -5٪ ، فإن القيمة المتوقعة للاستراتيجية هي:
(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04
يمكن استخدام التوزيع ذي الحدين لحساب احتمالات كل نتيجة محتملة في سلسلة من المعاملات الثنائية.
على سبيل المثال ، إذا أجرى متداول 10 صفقات ثنائية مع احتمال نجاح 60٪ واحتمال فشل 40٪ ، فيمكن حساب احتمال إجراء عدد معين من الصفقات الناجحة (أي معدل نجاح معين) باستخدام توزيع ثنائي.
يمكن أن يساعد هذا المتداول في تقييم المخاطر والعودة المحتملة لاستراتيجية التداول الخاصة به.
القيمة المتوقعة
لقد قمنا بتغطية القيمة المتوقعة (EV) في مقالات أخرى لأنها مفهوم أساسي في نظرية الاحتمالات التي تصف متوسط نتيجة متغير عشوائي.
في التداول والاستثمار ، يتم استخدام القيمة المتوقعة لحساب العائد والمخاطر المحتملة لاستراتيجية الاستثمار أو التداول.
رياضياً ، القيمة المتوقعة للمتغير العشوائي هي مجموع حاصل ضرب كل نتيجة محتملة واحتمالاتها.
على سبيل المثال ، ضع في اعتبارك رمية عملة معدنية تدفع دولارًا واحدًا للرؤوس و 0 دولارًا للذيول.
القيمة المتوقعة لهذا السحب كما يلي:
EV = (0.5 * 1 دولار) + (0.5 * 0 دولار) = 0.50 دولار
هذا يعني أن متوسط الدفع مقابل هذه العملة هو 0.50 دولار. سيعطيك هذا نقطة التعادل بمرور الوقت لأن احتمالاتك تتطابق مع الاحتمال الفعلي.
في التداول والاستثمار ، يتم استخدام القيمة المتوقعة لتقدير العوائد المحتملة من استراتيجية التداول أو الاستثمار.
على سبيل المثال ، إذا كان السهم لديه فرصة 60٪ لزيادة قيمته بنسبة 10٪ وفرصة بنسبة 40٪ لخفضه بنسبة 5٪ ، فيمكن حساب العائد المتوقع على الاستثمار على النحو التالي:
EV = (0.6 * 10٪) + (0.4 * -5٪) = 6٪ - 2٪ = 4٪
هذا يعني أن العائد المتوقع على الاستثمار هو 4٪.
يمكن أن تساعد هذه المعلومات المستثمرين والمتداولين على تحديد ما إذا كانوا سيستثمرون في الأسهم ، وتقييم المخاطر والعائد المحتمل لاستثماراتهم.
القيمة المتوقعة مهمة أيضًا في إدارة المخاطر.
من خلال حساب القيمة المتوقعة لاستراتيجية التداول أو الاستثمار ، يمكن للمتداولين والمستثمرين تقييم المخاطر المحتملة للاستثمار.
على سبيل المثال ، إذا كانت القيمة المتوقعة للاستثمار سلبية ، فهذا يعني أنه من المحتمل أن يخسر الاستثمار المال في المتوسط على المدى الطويل.
يمكن للمتداولين / المستثمرين استخدام هذه المعلومات لإدارة مخاطرهم عن طريق تنويع استثماراتهم أو الحد من تعرضهم للاستثمار أو المعاملة.
أيضًا ، كما غطينا أيضًا في مقالات أخرى ، فإن الرهان على النتيجة بأعلى قيمة متوقعة ليس دائمًا القرار الأفضل.
من الأفضل أحيانًا الحصول على قيمة متوقعة أقل إذا كانت تمنحك تباينًا أقل (مخاطر أقل للخسارة أو الفشل). أيضًا ، تريد دائمًا التأكد من أنه يمكنك تغطية الخسارة.
على سبيل المثال ، إذا كان لديك 1000 دولار ولديك فرصة 90٪ لمضاعفة أموالك إلى 2000 دولار وفرصة 10٪ لخسارة 1000 دولار بالكامل ، فإن PV الخاص بك مرتفع جدًا (1800 دولار - 1000 دولار = + 800 دولار).
ولكن إذا كنت لا تستطيع تحمل خسارة 1000 دولار في حالة الفوضى ، فمن الأفضل عدم اتخاذ القرار.
سلسلة ماركوف
سلسلة ماركوف هي مفهوم رياضي في نظرية الاحتمالات يصف عملية تعتمد فيها الخطوة أو الحالة التالية فقط على الحالة الحالية وليس على الحالات السابقة.
بمعنى آخر ، إنها عملية بلا ذاكرة تعتمد فقط على حالتها الحالية لتحديد حالتها المستقبلية.
يتم تعريف سلسلة ماركوف من خلال مجموعة من الحالات واحتمالات الانتقال من حالة إلى أخرى.
غالبًا ما يتم تمثيل هذه الاحتمالات في مصفوفة انتقالية ، حيث يمثل كل عنصر من عناصر المصفوفة احتمال الانتقال من حالة إلى أخرى.
تعتبر سلسلة ماركوف مهمة في مجال التداول / الاستثمار لأنه يمكن استخدامها لنمذجة سلوك الأسواق المالية.
سوق الأوراق المالية ، على سبيل المثال ، هو نظام معقد يحتوي على عدد كبير من المتغيرات التي تؤثر على سعر الأوراق المالية التي يتكون منها.
تتيح سلسلة ماركوف تبسيط النظام من خلال التركيز فقط على الحالة الحالية للسوق واحتمالات الانتقال إلى دول أخرى.
من خلال نمذجة سوق الأوراق المالية كسلسلة ماركوف ، يمكن للمتداولين والمستثمرين الحصول على منظور إضافي من خلال التنبؤ بحركات السوق المستقبلية بناءً على الحالة الحالية للسوق.
يمكن أيضًا استخدام سلسلة ماركوف للمساعدة في حساب المقاييس المختلفة مثل العوائد المتوقعة والتقلبات والمخاطر.
أيضًا ، تُستخدم سلسلة ماركوف في تقنيات النمذجة المالية المختلفة مثل تسعير الخيارات ، وتحسين المحفظة ، وإدارة المخاطر.
يسمح للمتداولين / المستثمرين بإنشاء واختبار استراتيجيات الاستثمار المختلفة ، وقياس فعالية هذه الاستراتيجيات في ظل ظروف السوق المختلفة.
مشي عشوائي
المشي العشوائي هو مفهوم رياضي من نظرية الاحتمالية التي تصف حركة كائن بطريقة عشوائية وغير متوقعة.
في نزهة عشوائية ، يتم تحديد الموضع التالي للكائن من خلال عملية عشوائية ، مثل سحب القرعة أو رمي النرد.
في مجال التمويل ، غالبًا ما يستخدم نموذج السير العشوائي لوصف تطور أسعار الأسهم بمرور الوقت.
النظرية الكامنة وراء هذا النموذج هي أن حركة سعر السهم لا يمكن التنبؤ بها وتتبع نمطًا عشوائيًا.
هذا يعني أن سعر السهم في أي وقت من المرجح أن يرتفع كما هو الحال مع الانخفاض ، وأن حركة سعر السهم بمرور الوقت لا تتأثر بالأسعار السابقة أو العوامل الخارجية الأخرى. (بالطبع ، هناك العديد من الأفكار والنظريات حول الاتجاهات والزخم وما إلى ذلك)
مفهوم المشي العشوائي مفيد في معرفته في مجال التداول والاستثمار لأنه يوحي بصعوبة التنبؤ بحركة أسعار الأسهم.
هذا يعني أنه من الصعب التغلب على السوق باستمرار عن طريق شراء وبيع الأسهم بناءً على تحركات الأسعار السابقة أو معلومات أخرى.
يمكن للمستثمرين والتجار استخدام مفهوم المشي العشوائي لدعم استراتيجية الاستثمار واتخاذ قرارات أكثر استنارة.
على سبيل المثال ، قد يختارون الاستثمار في محفظة متنوعة من الأسهم لتقليل تعرضهم لتحركات أسعار الأسهم الفردية والتنويع حسب الأصول وفئة الأصول والبلد والعملة ، والنظر في استخدام استراتيجية الشراء والاحتفاظ لتجنب التكاليف و مخاطر التداول المتكرر.
عملية العشوائية
العملية العشوائية هي إطار رياضي يستخدم لنمذجة سلوك نظام يتطور بشكل عشوائي بمرور الوقت.
إنها مجموعة من المتغيرات العشوائية المفهرسة بالوقت ، مما يعني أن قيمة العملية في أي وقت تكون عشوائية.
تعتبر العمليات العشوائية مفيدة في نظرية الاحتمالات لأنها يمكن أن تساعدنا في تحليل سلوك الظواهر العشوائية التي تتغير بمرور الوقت.
إنها توفر طريقة لنمذجة وفهم عشوائية هذه الظواهر ، والتي يمكن استخدامها لعمل تنبؤات واتخاذ قرارات بناءً على النتائج المتوقعة.
في مجال التجارة والاستثمار ، تُستخدم العمليات العشوائية لنمذجة سلوكيات معينة للأسواق المالية وأسعار الأصول.
إنها تساعد في تحليل عشوائية وتقلب البيانات المالية ، والتي يمكن استخدامها لاتخاذ قرارات بشأن وقت شراء أو بيع الأصول.
على سبيل المثال ، يمكن استخدام العمليات العشوائية لنمذجة حركة أسعار الأسهم أو أسعار صرف العملات ، والتي يمكن أن تساعد المتداولين والمستثمرين على وضع تنبؤات حول التحركات المستقبلية في هذه الأسواق.
تُستخدم العمليات العشوائية أيضًا لتطوير واختبار استراتيجيات التداول. من خلال محاكاة سلوك الأسواق المالية باستخدام العمليات العشوائية ، يمكن للمتداولين والمستثمرين اختبار استراتيجيات التداول الخاصة بهم وتقييم أدائهم في ظل ظروف السوق المختلفة.
احتمال مشروط
الاحتمال الشرطي هو مفهوم أساسي في نظرية الاحتمالات يشير إلى احتمال وقوع حدث إذا حدث بالفعل حدث آخر. إنها طريقة لتحديث تقديرات الاحتمالات الخاصة بنا بناءً على المعلومات الجديدة.
بشكل أكثر رسمية ، يتم تعريف الاحتمال الشرطي لحدث أ بالنظر إلى وقوع الحدث ب على النحو التالي:
الفوسفور (أ | ب) = الفوسفور (أ و ب) / ف (ب)
أو :
- P (A و B) هو احتمال وقوع الحدثين A و B ، و
- P (B) هو احتمال وقوع الحدث B.
يعد الاحتمال الشرطي مهمًا في التداول والاستثمار لأنه يسمح لنا بتحديث تقديرات الاحتمالية عند توفر معلومات جديدة.
على سبيل المثال ، إذا علمنا أن إحدى الشركات قد أعلنت للتو عن تقرير أرباح إيجابي ، فإن الاحتمال الشرطي لارتفاع سعر السهم في ضوء هذه المعلومات يكون أعلى مما كان عليه قبل الإعلان.
يستخدم المستثمرون والمتداولون الاحتمال الشرطي لاتخاذ قرارات أكثر استنارة بناءً على معلومات جديدة.
من خلال تحديث تقديرات الاحتمالات الخاصة بهم ، يمكنهم تقييم المخاطر والعوائد المحتملة لاستثمار معين بشكل أفضل.
يمكن أن يساعدهم هذا في إجراء صفقات أكثر ربحية وإدارة مخاطرهم بشكل أكثر فعالية.
على سبيل المثال ، افترض أن مستثمرًا يفكر في شراء سهم كان متقلباً تاريخياً.
باستخدام الاحتمال الشرطي ، يمكن للمستثمر تقييم احتمالية ارتفاع أو انخفاض سعر السهم بناءً على ظروف السوق المختلفة ، مثل التغيرات في أسعار الفائدة ، والنمو ، والتضخم ، والأحداث السياسية أو الجيوسياسية.
يمكن أن تساعد هذه المعلومات المستثمر في اتخاذ قرار أكثر استنارة بشأن شراء الأسهم أو الاحتفاظ بها أو بيعها.
قانون الأعداد الكبيرة
قانون الأعداد الكبيرة هو مفهوم أساسي في نظرية الاحتمالات يصف سلوك متوسط عدد كبير من المتغيرات العشوائية المستقلة.
ينص هذا القانون على أنه مع زيادة عدد المحاكمات المستقلة ، يتقارب متوسط تلك التجارب مع القيمة المتوقعة لتوزيع الاحتمالات الأساسي.
بعبارات أبسط ، ينص قانون الأعداد الكبيرة على أنه كلما تكررت التجربة ، كلما اقتربت النتائج المرصودة من النتيجة المتوقعة.
مثال على الرؤوس أو ذيول
على سبيل المثال ، إذا رميت عملة معدنية بشكل متكرر ، فإن قانون الأعداد الكبيرة يتنبأ بأن معدل تكرار الوجه سيقترب من 50٪ مع زيادة عدد الرميات.
أكثر من 1000 محاولة ، من غير المحتمل للغاية أن تحصل عملة عادلة على 55/45 في كلتا الحالتين (0.17٪) ، ولكن من الممكن بالتأكيد أكثر من 100 رمية (36.8٪).
لماذا هو مفيد
يعتبر قانون الأعداد الكبيرة مفيدًا في التداول والاستثمار لأنه يساعد في التخفيف من مخاطر تقلبات السوق غير المتوقعة.
من خلال الاستثمار في محفظة متنوعة ، يمكن للمستثمر توزيع مخاطره على عدد كبير من الأصول ، والتي يمكن أن تساعد في تقليل تأثير تحركات أسعار الأصول الفردية.
أيضًا ، يعد قانون الأعداد الكبيرة مفيدًا لتحليل بيانات السوق التاريخية لاتخاذ قرارات استثمارية مستنيرة.
من خلال دراسة عدد كبير من اتجاهات السوق التاريخية ، يمكن للمستثمرين المساعدة في تحديد الأنماط والاتجاهات التي يمكن أن تساعدهم في اتخاذ قرارات استثمارية أكثر استنارة.
على سبيل المثال ، إذا أراد أحد المتداولين معرفة ما إذا كان الاحتياطي الفيدرالي قد خفض أسعار الفائدة على الرغم من التضخم فوق الهدف ، فيمكنه النظر إلى التاريخ لمعرفة ما إذا كانت هناك أي سوابق والتأثير الذي أحدثه هذا في أسواق الأصول المختلفة.
إذا كانت هناك عينة ، فما حجم الحصول على بيانات مفيدة كافية لتحديد الاستنتاجات المفيدة؟
كيف يرتبط قانون الأعداد الكبيرة بالدلالة الإحصائية؟
يعتبر قانون الأعداد الكبيرة والأهمية الإحصائية مفاهيم مرتبطة في الإحصاء ، لكنهما ليسا متشابهين.
يشير قانون الأعداد الكبيرة إلى حقيقة أن متوسط العينة لعدد كبير من الملاحظات المستقلة يتقارب مع القيمة المتوقعة لتوزيع الاحتمالات الأساسي ، حيث يقترب عدد الملاحظات من اللانهاية.
من ناحية أخرى ، فإن الأهمية الإحصائية هي مقياس لاحتمال أن النتائج المرصودة للدراسة ليست بسبب الصدفة.
في اختبار الفرضيات الإحصائية ، تعتبر النتيجة ذات دلالة إحصائية إذا كان احتمال الحصول على النتيجة المرصودة بالصدفة أقل من عتبة محددة مسبقًا ، عادةً 5٪ أو أقل.
في الممارسة العملية ، يمكن استخدام قانون الأعداد الكبيرة لدعم الدلالة الإحصائية.
عندما يتم جمع عينة كبيرة ويكون متوسط العينة قريبًا من القيمة المتوقعة للتوزيع الأساسي ، فإن هذا يشير إلى أن النتائج المرصودة أقل احتمالًا لأن تكون بسبب الصدفة وأكثر احتمالًا أن تكون ذات دلالة إحصائية.
ومع ذلك ، من المهم ملاحظة أن الأهمية الإحصائية لا تعني بالضرورة أهمية عملية أو أهمية اقتصادية ، ولا ينبغي استخدام الأهمية الإحصائية وحدها لاتخاذ قرارات مهمة.
لاتخاذ قرارات مستنيرة ، من الضروري أن يكون لديك فهم جيد للبيانات الأساسية والأساليب الإحصائية وسياق المشكلة قيد الدراسة.
مبرهنة بايز
نظرية بايز هي مفهوم أساسي في نظرية الاحتمالات التي تصف كيفية تحديث الاحتمالات بناءً على أدلة أو معلومات جديدة.
ويعود اسمها إلى القس توماس بايز ، وهو إحصائي وعالم لاهوت بريطاني من القرن الثامن عشر.
توفر النظرية طريقة لحساب احتمال فرضية أو حدث بناءً على المعرفة أو المعتقدات السابقة (تسمى الاحتمال السابق) والأدلة الجديدة (تسمى الاحتمالية).
يسمى الاحتمال المخصوم الاحتمال اللاحق ، وهو يمثل احتمال الفرضية أو الحدث بعد الأخذ في الاعتبار الدليل الجديد.
صيغة نظرية بايز هي:
الفوسفور (A | B) = P (B | A) * P (A) / P (B)
أو :
- P (A | B) هو الاحتمال اللاحق للحدث A معطى الدليل B
- P (B | A) هو احتمال الإثبات B معطى الحدث A
- P (A) هو الاحتمال السابق للحدث A ، و
- P (B) هو احتمال الإثبات B
نظرية بايز مفيدة في مجال التداول والاستثمار لأنها يمكن أن تساعد المستثمرين على تحديث معتقداتهم حول احتمالية الأحداث المختلفة بناءً على معلومات جديدة ، مثل أخبار أرباح الشركة أو الأعمال أو المؤشرات الاقتصادية.
وهذا جانب أساسي من جوانب احتمالية بايز: فهو يُحدِّث معتقداتك السابقة ، دون الحاجة إلى تحديدها أو إعادة حسابها من الصفر.
باستخدام نظرية بايز ، يمكن للمستثمرين تحديث احتمالاتهم واتخاذ قرارات استثمارية أكثر استنارة.
أمثلة على أهمية التحقق من افتراضاتنا
أمين صندوق البنك
يأتي أحد الأمثلة الشهيرة على نظرية بايز في العمل من دراسة كانيمان وتفيرسكي.
في هذه الدراسة ، تلقى المشاركون المعلومات التالية:
ليندا تبلغ من العمر 31 عامًا ، عازبة ، صريحة وذكية جدًا. درست الفلسفة. كطالبة ، كانت قلقة للغاية بشأن قضايا التمييز والعدالة الاجتماعية ، وشاركت أيضًا في الاحتجاجات المناهضة للأسلحة النووية.
ثم طُلب من المشاركين ترتيب احتمالية وجود سيناريوهين محتملين:
- ليندا صراف بنك.
- ليندا صراف بنك وناشطة في الحركة النسوية.
على الرغم من حقيقة أن السيناريو الأول يتضمن عددًا أكبر من الأشخاص (جميع الصرافين) مقارنة بالسيناريو الثاني (الصراف والنسوية) ، فقد صنف العديد من المشاركين السيناريو الثاني على أنه أكثر احتمالًا.
هذا لأن وصف ليندا يناسب صورتها النمطية النسوية ، على الرغم من أن احتمال وقوع الحدثين أقل من احتمال وقوع الحدث الأول.
يوضح هذا المثال أهمية التحقق من افتراضاتنا والنظر في جميع المعلومات المتاحة قبل اتخاذ القرارات.
يمكن أن تساعد نظرية بايز المستثمرين في تحديث احتمالاتهم وتجنب التحيزات التي يمكن أن تؤدي إلى قرارات غير صحيحة.
هل ستيف مزارع أم أمين مكتبة؟
تضمنت الدراسة الشهيرة التي أجراها كانيمان وتفيرسكي سيناريو آخر كان على المشاركين فيه تحديد احتمال أن يكون ستيف إما مزارعًا أو أمين مكتبة ، بناءً على معلومات محدودة عن شخصيته.
تلقى المشاركون المعلومات التالية:
ستيف شخص هادئ وخجول يحب قراءة الكتب وليس اجتماعيًا جدًا.
بناءً على هذه المعلومات وحدها ، خلص معظم المشاركين إلى أن ستيف كان من المرجح أن يكون أمين مكتبة أكثر من كونه مزارعًا. ومع ذلك ، أظهر كانيمان وتفيرسكي أن هذا الاستنتاج لم يكن مبررًا بالضرورة.
لإثبات ذلك ، قدموا للمشاركين معلومات إضافية كانت ذات صلة ولكن لم يتم تضمينها في الوصف الأولي.
على سبيل المثال ، أضافوا معلومات عن عدد المزارعين مقابل أمناء المكتبات والنسبة المئوية للمزارعين من نوع شخصية ستيف ، والتي لا تزال تعطي عددًا أكبر من المزارعين عن العدد الإجمالي لأمناء المكتبات.
على سبيل المثال ، إذا كان عدد المزارعين 20 ضعفًا عن أمناء المكتبات و 20٪ من المزارعين يتناسبون مع هذا النوع من الشخصية ، فلا يزال احتمال أن يكون ستيف مزارعًا 4 مرات (20 * 0.20) أكثر من كونه أمين مكتبة.
عندما تلقى المشاركون هذه المعلومات الجديدة ، زادت احتمالات أن يكون ستيف مزارعًا بشكل ملحوظ ، مما يشير إلى أن استنتاجاتهم الأولية لم تكن على دراية كافية.
تسلط هذه الدراسة الضوء على أهمية اختبار الافتراضات عند اتخاذ القرارات بناءً على معلومات محدودة.
من المهم مراعاة جميع العوامل ذات الصلة وعدم الاعتماد فقط على الافتراضات الأولية أو الاستدلال ، مثل القوالب النمطية ، عند اتخاذ القرارات أو تشكيل الأحكام.
يتوافق هذا النهج مع النهج البايزي للاحتمالية ، والذي يتضمن تحديثًا مستمرًا للمعتقدات بناءً على معلومات جديدة.
في التداول والاستثمار ، من المهم دائمًا أن تسأل كيف تعرف أنك تعرف؟
الارتباط والتغاير
الارتباط والتغاير هما مفهومان إحصائيان شائعان في نظرية الاحتمالات لوصف العلاقة بين متغيرين عشوائيين.
يقيس التباين مدى تحرك متغيرين عشوائيين معًا ، بينما يقيس الارتباط قوة واتجاه علاقتهما.
يشير التغاير الموجب إلى أن المتغيرين يميلان إلى التحرك في نفس الاتجاه ، بينما يشير التباين السلبي إلى أنهما يميلان إلى التحرك في اتجاهين متعاكسين.
يتراوح معامل الارتباط من -1 إلى 1 ، حيث تشير القيم 1 إلى ارتباط إيجابي مثالي ، وتشير قيم -1 إلى ارتباط سلبي مثالي ، وتشير قيم 0 إلى عدم وجود ارتباط.
في مجال التداول / الاستثمار ، يعتبر الارتباط والتباين المشترك أدوات مفيدة لإدارة المخاطر وتنويع المحفظة.
من خلال فهم العلاقة بين الأصول المختلفة ، يمكن للمستثمرين إدارة محافظهم بشكل أفضل عن طريق اختيار الأصول التي لا ترتبط ارتباطًا وثيقًا ببعضها البعض.
يمكن أن يساعد ذلك في تقليل مخاطر المحفظة الإجمالية من خلال توزيع الاستثمارات عبر فئات الأصول والقطاعات المختلفة.
على سبيل المثال ، قد تكون محفظة الأسهم ذات الارتباط العالي ببعضها البعض أكثر خطورة من محفظة الأسهم أو الأصول الأخرى ذات الارتباط المنخفض مع بعضها البعض.
من خلال اختيار مجموعة متنوعة من الأصول منخفضة الارتباط ، يمكن للمستثمر إنشاء محفظة أكثر مرونة من غير المرجح أن تتكبد خسائر كبيرة في حالة الانكماش في السوق.
بالإضافة إلى ذلك ، يمكن أن يساعد فهم الارتباط والتغاير المستثمرين على تحديد الأنماط في السوق والتنبؤ بالاتجاهات المستقبلية.
من المهم أيضًا أن نفهم أن الارتباطات تكون بأثر رجعي وتميل إلى التغيير بمرور الوقت.
على سبيل المثال ، قد ترتبط الأسهم والسندات ارتباطًا سلبيًا في بيئة تتناقص فيها التغيرات في التضخم المخصوم ، ولكن قد تكون مرتبطة بشكل إيجابي في البيئات التي يتزايد فيها التضخم المخصوم.
وبالتالي ، فإن التفسيرات الأكثر قوة للتضخم ستنظر عن كثب في الحالة الجوهرية للأصول بناءً على الروابط الاقتصادية القائمة على السبب والنتيجة ، بدلاً من التفسيرات المتخلفة مثل معاملات الارتباط البسيطة ، والتي هي مجرد منتجات هدامة للبيئة التي تم ايجادهم.
وسطاء CFD
الأسئلة الشائعة - نظرية الاحتمالية في التداول
ما هي نظرية الاحتمالات ولماذا هي مهمة في التداول؟
نظرية الاحتمالية هي فرع من فروع الرياضيات التي تتعامل مع تحليل الظواهر العشوائية.
يوفر إطارًا لفهم احتمالية الأحداث وسلوك الأنظمة التي تظهر العشوائية.
نظرية الاحتمالية هي أداة أساسية لاتخاذ قرارات مستنيرة في المواقف التي تكون فيها النتيجة غير مؤكدة.
في التداول ، تعتبر نظرية الاحتمالات ضرورية لفهم المخاطر والعوائد المحتملة لاستراتيجيات الاستثمار المختلفة.
يستخدم المتداولون نظرية الاحتمالات لتقييم احتمالية وقوع أحداث معينة ، مثل احتمال ارتفاع قيمة السهم أو وقوع حدث مهم.
يستخدمونها أيضًا لحساب القيمة المتوقعة لصفقاتهم ، وهي متوسط الربح أو الخسارة التي يمكن أن يتوقعوا تحقيقها على المدى الطويل.
باستخدام نظرية الاحتمالات ، يمكن للمتداولين اتخاذ قرارات أكثر استنارة حول وقت الدخول أو الخروج من الصفقة ، ومقدار الاستثمار ، وكيفية إدارة المخاطر.
يمكنهم أيضًا استخدامها لتطوير واختبار استراتيجيات التداول لمعرفة كيفية أدائها في ظروف السوق المختلفة.
ما هي أهم مفاهيم الاحتمالات التي يجب على المتداولين فهمها؟
هناك العديد من مفاهيم الاحتمالات المهمة التي يحتاج المتداولون إلى فهمها.
وهنا عدد قليل :
- التوزيعات الاحتمالية: تصف التوزيعات الاحتمالية احتمالية النتائج المختلفة في حدث عشوائي. يستخدم المتداولون التوزيعات الاحتمالية لفهم النطاق المحتمل للنتائج لصفقة معينة. توزيعات الاحتمالية المستخدمة بشكل شائع في التداول تشمل التوزيع الطبيعي ، الذي يصف سلوك العديد من المتغيرات المالية ، والتوزيع ذي الحدين ، والذي يستخدم لنمذجة النتائج الثنائية.
- القيمة المتوقعة: القيمة المتوقعة للمعاملة هي متوسط الربح أو الخسارة الذي يمكن توقعه على المدى الطويل. من خلال حساب القيمة المتوقعة ، يمكن للمتداولين قياس الربحية المحتملة للتداول واتخاذ قرارات أكثر استنارة حول الدخول أو الخروج من الصفقة.
- الانحراف المعياري: الانحراف المعياري هو مقياس لمقدار التباين أو التقلب في مجموعة البيانات. يستخدم المتداولون الانحراف المعياري لفهم مستوى المخاطرة المرتبط بصفقة معينة. تشير المستويات الأعلى من الانحراف المعياري إلى مستويات أعلى من المخاطر. لاحظ أن الانحراف المعياري يستند إلى التوزيع الطبيعي ، والذي لا يتوافق مع العديد من الأصول المالية / النتائج المتغيرة.
- الارتباط: الارتباط يقيس قوة واتجاه العلاقة بين متغيرين. في التداول ، يستخدم المتداولون الارتباط لفهم كيفية تحرك الأصول المختلفة ضد بعضها البعض. يشير الارتباط الإيجابي العالي بين أصلين إلى أنهما يميلان إلى التحرك في نفس الاتجاه ، بينما يشير الارتباط السلبي إلى أنهما يميلان إلى التحرك في اتجاهين متعاكسين.
- الدلالة الإحصائية: تشير الدلالة الإحصائية إلى احتمال ألا تكون النتيجة المرصودة ناتجة عن صدفة. يستخدم المتداولون الدلالة الإحصائية لتقييم فعالية استراتيجية التداول أو لتحديد ما إذا كان من المحتمل أن يكون لحدث معين تأثير كبير على السوق.
يمكن أن يساعد فهم هذه المفاهيم وغيرها من مفاهيم الاحتمالات المتداولين على اتخاذ قرارات أفضل في الأسواق وإدارة مخاطرهم بشكل أكثر فعالية.
الاستنتاج - نظرية الاحتمالية في التداول
تلعب نظرية الاحتمالية دورًا مهمًا في التداول لأنها تساعد المتداولين على اتخاذ قرارات مستنيرة استنادًا إلى التحليل المستند إلى البيانات.
باستخدام نظرية الاحتمالات ، يمكن للمتداولين تقدير احتمالية تحركات السوق المحتملة وتطوير استراتيجيات تداول للاستفادة من تلك التحركات.
يساعد المتداولين على تقييم نسبة المخاطرة والمكافأة للتداول وإدارة محافظهم وتحسين مراكزهم.
تعتبر نظرية الاحتمالية مفيدة بشكل خاص لقياس عدم اليقين وقياس تقلبات السوق ، مما يسمح للمتداولين بالتنبؤ والاستعداد لتغيرات السوق.
بشكل عام ، توفر نظرية الاحتمالات للمتداولين الأدوات اللازمة لاتخاذ قرارات تداول أكثر استنارة ودقة ، مما قد يؤدي إلى تحسين الربحية وتقليل المخاطر.
| سابق : التباين المشترك - تطبيقات في التداول وبناء المحفظة | التالية : كيفية بناء نظام تجاري |


