Teoría de la probabilidad y trading

¿Qué es la teoría de la probabilidad y por qué es importante?

La teoría de la probabilidad es esencial en el trading y la inversión porque permite a los participantes en el mercado comprender y cuantificar la incertidumbre y el riesgo asociados a las decisiones financieras.

Como la vida misma, el trading es un juego de probabilidades. Rara vez hay resultados obvios, en blanco y negro, que sean fáciles de capitalizar.

Utilizando la teoría de la probabilidad, los traders e inversores pueden tomar decisiones más informadas basándose en la probabilidad de diversos resultados.

He aquí algunas razones por las que la teoría de la probabilidad es tan importante en el trading y la inversión:

Cuantificación del riesgo

La teoría de la probabilidad permite a los inversores calcular la probabilidad de que ocurran varias cosas, incluidos los escenarios positivos y negativos.

Esto permite a los traders comprender mejor los riesgos potenciales asociados a las distintas operaciones/inversiones.

Toma de decisiones

La teoría de la probabilidad permite a los traders tomar mejores decisiones basándose en la probabilidad de que se produzcan distintos resultados y evaluando las propias probabilidades (lo que podría denominarse "probabilidad de probabilidades", ya que las probabilidades de que se produzcan distintas cosas no se conocen por sí mismas).

Por ejemplo, si una inversión o transacción tiene una probabilidad del 70% de producir un rendimiento positivo a lo largo de un año, ¿cómo se sabe?

La teoría de la probabilidad abarca aspectos como la varianza y cómo gestionar mejor lo que no se sabe y no se puede saber.

Gestión de carteras

La teoría de la probabilidad ayuda a los traders/inversores a gestionar sus carteras, ya que permite evaluar el riesgo asociado a las distintas clases de activos.

Analizando la probabilidad de diferentes resultados, los operadores/inversores pueden crear una cartera diversificada que equilibre riesgo y rentabilidad.

Gestión del riesgo

La teoría de la probabilidad también es importante en la gestión del riesgo, ya que ayuda a los inversores a determinar la probabilidad de que se produzcan acontecimientos que podrían afectar negativamente a sus inversiones/operaciones y a tomar medidas para mitigarlos.

En general, la teoría de la probabilidad es una herramienta importante para que los inversores/traders comprendan los riesgos y beneficios potenciales de las distintas oportunidades de inversión, tomen decisiones con mayor conocimiento de causa y consigan mejores resultados a largo plazo.

En este artículo, examinaremos las distintas ramas de la teoría de la probabilidad y sus aplicaciones en el trading.

Azar

En la teoría de la probabilidad, la aleatoriedad se refiere al hecho de que el resultado de un suceso es impredecible y puede variar de un ensayo a otro.

Este fenómeno suele modelizarse mediante distribuciones de probabilidad, que describen la probabilidad de cada resultado posible.

El azar es un concepto fundamental en la teoría de la probabilidad porque nos permite cuantificar lo desconocido y hacer predicciones sobre el futuro a partir de información incompleta.

En muchas situaciones del mundo real, los resultados de los acontecimientos se ven afectados por un gran número de variables que son difíciles o imposibles de predecir con certeza/precisión.

La aleatoriedad nos permite tener esto en cuenta y estimar la probabilidad de diversos resultados basándonos en datos históricos, causalidad económica u otra información.

En el trading y la inversión, la aleatoriedad está siempre presente porque los mercados financieros están sujetos a una amplia gama de influencias.

En los mercados hay muchos tipos diferentes de personas, de distintos tamaños y con distintas motivaciones para operar.

La aleatoriedad puede manifestarse en forma de volatilidad del mercado, acontecimientos inesperados u otros factores que pueden provocar movimientos de precios rápidos e imprevisibles.

Comprender y tener en cuenta esta aleatoriedad es esencial para desarrollar estrategias de trading exitosas y gestionar el riesgo.

Cuanta más experiencia adquieren las personas en los mercados, más se dan cuenta de que todo lo que saben palidece en comparación con las cosas que necesitan saber en función de lo que se actualiza en los mercados.

Una forma en que los traders y los inversores pueden hacer frente a la aleatoriedad es utilizar modelos basados en probabilidades para tomar decisiones.

Por ejemplo, un operador puede utilizar un modelo estadístico para estimar la probabilidad de que suba o baje el precio de un activo concreto en un periodo determinado. Esta información puede utilizarse para construir una cartera equilibrada y gestionar el riesgo.

Por ejemplo, si la distribución de precios descontados de un activo concreto tiene el siguiente aspecto

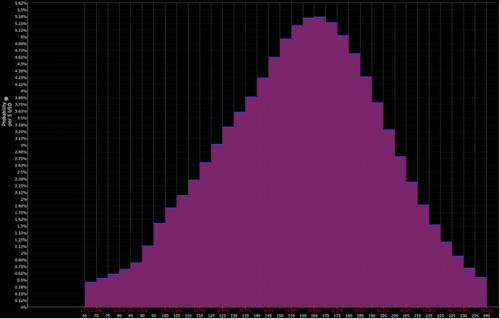
Y la interpretación del operador se acerca más a la combinación de la distribución roja y morada (es decir, una inclinación bajista):

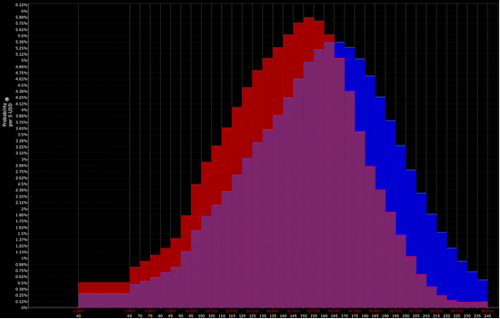
En ese caso, pueden esperar tomar una posición bajista en el activo. Luego, por supuesto, está la cuestión de cómo establecerla y el tamaño.

Exclusividad mutua

En la teoría de la probabilidad, el concepto de exclusividad mutua se refiere a la propiedad de dos sucesos que son diferentes entre sí.

Matemáticamente, se dice que dos sucesos A y B son mutuamente excluyentes si su intersección (es decir, el suceso en el que ocurren tanto A como B) está vacía, es decir, P(A ∩ B) = 0.

La exclusividad mutua es importante en el trading y la inversión porque ayuda a los inversores a comprender mejor cómo gestionar sus riesgos.

Cuando los inversores tienen una cartera de activos, deben tener en cuenta las correlaciones entre sus activos.

Por ejemplo, supongamos que un operador/inversor tiene una cartera de acciones que incluye empresas tecnológicas y petroleras. Si el precio del petróleo sube, esto puede ayudar a las petroleras, pero las acciones tecnológicas pueden sufrir (por ejemplo, debido al efecto negativo de la subida de los precios del petróleo en los tipos de interés), y viceversa.

Sin embargo, si se producen avances en cada sector, es posible que no influyan en los precios de los valores del otro sector.

Así pues, aunque los valores están relacionados entre sí en algunos aspectos -como los cambios en el crecimiento descontado y la inflación-, en otros aspectos son mutuamente excluyentes.

¿Cómo se separan estos factores mutuamente excluyentes?

A veces se trata simplemente de la naturaleza del flujo financiero - por ejemplo, petróleo frente a productos/servicios tecnológicos.

A veces se denominan factores - por ejemplo, impulso, tamaño, calidad, valor, etc.

Además, la exclusividad mutua es importante en el trading de opciones, donde el beneficio de una opción puede basarse a menudo en la no ocurrencia de otro evento. En este contexto, la exclusividad mutua ayuda a los operadores a cubrir sus riesgos y gestionar su exposición.

Experimento (ensayo de Bernoulli)

Un experimento o ensayo de Bernoulli es un concepto fundamental de la teoría de la probabilidad que se refiere a un suceso aleatorio con sólo dos resultados posibles.

Por ejemplo, lanzar una moneda es un ensayo de Bernoulli, en el que los resultados posibles son cara o cruz.

Otro ejemplo es si una determinada operación de opciones será rentable (in-the-money) o no (out-of-the-money) al vencimiento.

En la teoría de la probabilidad, la probabilidad de éxito (es decir, el resultado de interés) se define por p, y la probabilidad de fracaso (es decir, el resultado alternativo) por q = 1 - p.

Los resultados de un ensayo Bernoulli suelen denotarse como 1 para el éxito y 0 para el fracaso.

La importancia de los ensayos de Bernoulli en el comercio y la inversión radica en que algunas decisiones financieras implican resultados binarios.

Por ejemplo, puede decidir comprar una opción sobre una acción con la esperanza de que alcance el punto de equilibrio, o puede decidir venderla con la esperanza de que su precio alcance el punto de equilibrio y reciba toda la prima.

En cualquier caso, el resultado es binario en términos de dinero. Las apuestas binarias puras adoptan la forma de opciones binarias.

Aplicando los principios de la teoría de la probabilidad al trading y a la inversión, puede tomar decisiones más informadas sobre cuándo comprar o vender.

También existen conceptos como el valor esperado, que le enseñan a no apostar siempre por el resultado más probable.

Distribución de probabilidades

En la teoría de la probabilidad, una distribución de probabilidad es una función que describe la probabilidad de diferentes resultados en un experimento o proceso aleatorio.

Especifica las probabilidades de todos los resultados posibles de un suceso, y la suma de las probabilidades de todos los resultados es igual a uno.

Existen muchos tipos de distribuciones de probabilidad, pero las más comunes son la distribución normal, la distribución binomial y la distribución de Poisson.

Cada distribución tiene su propio conjunto de parámetros que determinan su forma, y estos parámetros se utilizan a menudo para hacer predicciones y tomar decisiones.

Por supuesto, en los mercados financieros, los rendimientos suelen tener colas más anchas y no se ajustan a una distribución predeterminada, por lo que tienden a personalizarse.

En general, las distribuciones de probabilidad son importantes porque proporcionan un marco para comprender el riesgo y la incertidumbre asociados a las inversiones financieras.

Uno de los conceptos más importantes en el trading/inversión es que todo es una probabilidad (es decir, una distribución de resultados potenciales). No existe un resultado especialmente probable.

Utilizando distribuciones de probabilidad, los traders e inversores pueden estimar la probabilidad de diferentes resultados y tomar decisiones más informadas sobre cómo asignar sus recursos.

Por ejemplo, un trader puede utilizar la distribución normal o una distribución de cola gruesa para modelizar los rendimientos diarios de una acción concreta.

A continuación, podría utilizar esta distribución para estimar la probabilidad de que el rendimiento de la acción supere un determinado umbral, por ejemplo, un rendimiento de +/-5% en un día.

Utilizando las distribuciones de probabilidad de este modo, los traders pueden gestionar mejor su riesgo y optimizar sus beneficios.

Además de estimar probabilidades, las distribuciones de probabilidad también se utilizan para crear instrumentos financieros como opciones y futuros.

Estos instrumentos tienen un precio basado en la distribución subyacente del activo al que están vinculados, y los traders pueden utilizarlos para cubrir su riesgo o hacer apuestas sobre futuros movimientos del precio del activo.

Además, pueden construirse distribuciones basadas en el precio de las opciones subyacentes, como se muestra a continuación.

Distribución descontada por los mercados :

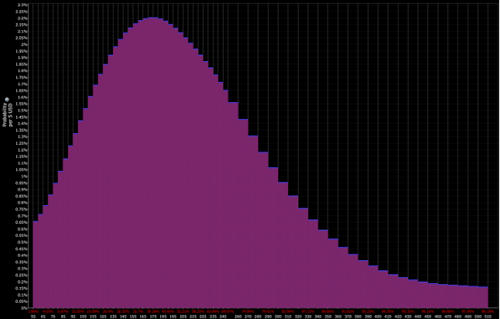
Distribución determinada por el trader (lo que abre la puerta a oportunidades tácticas):

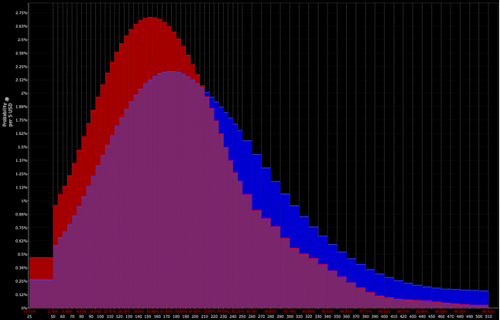
Distribución binomial

La distribución binomial es una distribución de probabilidad que modela el número de resultados positivos en una serie de ensayos independientes e idénticos, donde cada ensayo tiene sólo dos resultados posibles (por ejemplo, cara o cruz, ganar o perder, alto o bajo).

Los parámetros clave de la distribución binomial son la probabilidad de éxito en un único ensayo (denominada p) y el número de ensayos (denominado n).

La distribución binomial es importante en el campo del trading y la inversión porque puede utilizarse para modelar la distribución de los beneficios de una estrategia de trading binario (por ejemplo, una estrategia que consiste en comprar o vender un activo en función de si se produce un determinado evento).

En concreto, el valor esperado de una estrategia de trading binario puede calcularse utilizando la distribución binomial.

El valor esperado de una estrategia de trading binario es la suma de los productos de la probabilidad de cada resultado posible y el rendimiento de ese resultado.

Por ejemplo, si una estrategia de trading binario tiene una probabilidad del 60% de obtener una rentabilidad del 10% y una probabilidad del 40% de obtener una rentabilidad del -5%, el valor esperado de la estrategia es

(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04

La distribución binomial puede utilizarse para calcular las probabilidades de cada resultado posible en una serie de operaciones binarias.

Por ejemplo, si un trader realiza 10 operaciones binarias con una probabilidad de éxito del 60% y una probabilidad de fracaso del 40%, la probabilidad de realizar un determinado número de operaciones con éxito (es decir, una determinada tasa de éxito) puede calcularse utilizando la distribución binomial.

Esto puede ayudar al trader a evaluar el riesgo y la rentabilidad potencial de su estrategia de trading.

Valor esperado

Ya hemos hablado del valor esperado (VE) en otros artículos, ya que es un concepto fundamental de la teoría de la probabilidad que describe el resultado medio de una variable aleatoria.

En el ámbito del trading y la inversión, el valor esperado se utiliza para calcular la rentabilidad y el riesgo potenciales de una inversión o estrategia de trading.

Matemáticamente, el valor esperado de una variable aleatoria es la suma de los productos de cada resultado posible y su probabilidad.

Por ejemplo, consideremos el lanzamiento de una moneda que da 1 $ si sale cara y 0 $ si sale cruz.

El valor esperado de este lanzamiento es el siguiente:

VE = (0,5 * 1 $) + (0,5 * 0 $) = 0,50 $.

Esto significa que el pago medio para este lanzamiento de moneda es de 0,50 $. Esto le dará un punto de equilibrio a lo largo del tiempo, ya que sus probabilidades coinciden con la probabilidad real.

En el trading y la inversión, el valor esperado se utiliza para estimar el rendimiento potencial de una estrategia de trading o inversión.

Por ejemplo, si una acción tiene una probabilidad del 60% de aumentar su valor en un 10% y una probabilidad del 40% de disminuir su valor en un 5%, el rendimiento esperado de la inversión puede calcularse de la siguiente manera:

VE = (0,6 * 10%) + (0,4 * -5%) = 6% - 2% = 4%.

Esto significa que la rentabilidad esperada de la inversión es del 4%.

Esta información puede ayudar a los inversores y comerciantes a decidirse a invertir en la acción, y a evaluar el riesgo y el rendimiento potencial de su inversión.

El valor esperado también es importante en la gestión del riesgo.

Calculando el valor esperado de una estrategia de trading o de una inversión, los traders y los inversores pueden evaluar el riesgo potencial de la inversión.

Por ejemplo, si el valor esperado de una inversión es negativo, significa que es probable que la inversión pierda dinero por término medio a largo plazo.

Los traders/inversores pueden utilizar esta información para gestionar su riesgo diversificando sus inversiones o limitando su exposición a la inversión o transacción.

Además, como también hemos comentado en otros artículos, apostar por el resultado con el valor esperado más alto no siempre es la mejor decisión.

A veces es mejor tener un valor esperado más bajo si ello le proporciona una varianza menor (menor riesgo de pérdida o fracaso). Además, siempre hay que asegurarse de poder cubrir las pérdidas.

Por ejemplo, si tiene 1.000 $ y tiene un 90% de probabilidades de duplicar su dinero hasta 2.000 $ y un 10% de probabilidades de perder la totalidad de los 1.000 $, su VE es muy alto (1.800 $ - 1.000 $ = + 800 $).

Pero si no puede permitirse perder los 1.000 $ en caso de equivocarse, es mejor no tomar la decisión.

Cadena de Markov

La cadena de Markov es un concepto matemático de la teoría de la probabilidad que describe un proceso en el que el siguiente paso o estado sólo depende del estado actual y no de los estados anteriores.

En otras palabras, es un proceso sin memoria que sólo depende de su estado actual para determinar su estado futuro.

Una cadena de Markov se define por un conjunto de estados y las probabilidades de pasar de un estado a otro.

Estas probabilidades suelen representarse en una matriz de transición, donde cada elemento de la matriz representa la probabilidad de pasar de un estado a otro.

La cadena de Markov es importante en el campo del trading/inversión porque puede utilizarse para modelizar el comportamiento de los mercados financieros.

El mercado de valores, por ejemplo, es un sistema complejo con un gran número de variables que afectan al precio de los valores que lo componen.

La cadena de Markov permite simplificar el sistema centrándose únicamente en el estado actual del mercado y en las probabilidades de pasar a otros estados.

Al modelizar el mercado bursátil como una cadena de Markov, los traders e inversores pueden obtener información adicional al predecir los movimientos futuros del mercado basándose en el estado actual del mercado.

La cadena de Markov también puede utilizarse para calcular diversas medidas, como la rentabilidad esperada, la volatilidad y el riesgo.

Además, la cadena de Markov se utiliza en diversas técnicas de modelización financiera, como la valoración de opciones, la optimización de carteras y la gestión de riesgos.

Permite a los traders/inversores crear y probar distintas estrategias de inversión, y medir la eficacia de estas estrategias en distintas condiciones de mercado.

Recorrido aleatorio

El paseo aleatorio es un concepto matemático de la teoría de la probabilidad que describe el movimiento de un objeto de forma aleatoria e impredecible.

En un paseo aleatorio, la siguiente posición del objeto viene determinada por un proceso aleatorio, como el lanzamiento de una moneda o un dado.

En finanzas, un modelo de paseo aleatorio se utiliza a menudo para describir la evolución de los precios de las acciones a lo largo del tiempo.

La teoría en la que se basa este modelo es que el movimiento de los precios de las acciones es impredecible y sigue un patrón aleatorio.

Esto significa que el precio de una acción en un momento dado tiene las mismas probabilidades de subir que de bajar, y que el movimiento del precio de la acción a lo largo del tiempo no está influido por precios anteriores u otros factores externos. (Por supuesto, existen diversas ideas y teorías sobre tendencias, impulso, etc.).

Es útil conocer el concepto de paseo aleatorio en el trading y la inversión porque sugiere que es muy difícil predecir la evolución de los precios de las acciones.

Esto significa que es difícil batir sistemáticamente al mercado comprando y vendiendo acciones basándose en los movimientos pasados de los precios u otra información.

Los inversores y traders pueden utilizar el concepto de recorrido aleatorio para apoyar su estrategia de inversión y tomar decisiones más informadas.

Por ejemplo, pueden optar por invertir en una cartera diversificada de acciones para reducir su exposición a los movimientos individuales de los precios de las acciones y diversificar por activos, clases de activos, países y divisas, y considerar el uso de una estrategia de comprar y mantener para evitar los costes y riesgos de la negociación frecuente.

Proceso estocástico

El proceso estocástico es un marco matemático utilizado para modelizar el comportamiento de un sistema que evoluciona aleatoriamente en el tiempo.

Es una colección de variables aleatorias indexadas por el tiempo, lo que significa que el valor del proceso en un momento dado es aleatorio.

Los procesos estocásticos son útiles en la teoría de la probabilidad porque pueden ayudarnos a analizar el comportamiento de fenómenos aleatorios que evolucionan con el tiempo.

Proporcionan una forma de modelizar y comprender la aleatoriedad de estos fenómenos, que puede utilizarse para hacer predicciones y tomar decisiones basadas en los resultados esperados.

En el ámbito del trading y la inversión, los procesos estocásticos se utilizan para modelizar determinados comportamientos de los mercados financieros y los precios de los activos.

Permiten analizar la aleatoriedad y la volatilidad de los datos financieros, que pueden utilizarse para tomar decisiones sobre cuándo comprar o vender activos.

Por ejemplo, los procesos estocásticos pueden utilizarse para modelizar el movimiento de los precios de las acciones o los tipos de cambio, lo que puede ayudar a los operadores e inversores a hacer predicciones sobre futuros movimientos en estos mercados.

Los procesos estocásticos también se utilizan para desarrollar y probar estrategias de trading. Al simular el comportamiento de los mercados financieros mediante procesos estocásticos, los traders e inversores pueden poner a prueba sus estrategias de trading y evaluar su rendimiento en distintas condiciones de mercado.

Probabilidad condicional

La probabilidad condicional es un concepto fundamental de la teoría de la probabilidad que se refiere a la probabilidad de que ocurra un suceso si ya ha ocurrido otro. Es una forma de actualizar nuestras estimaciones de probabilidad a partir de nueva información.

Más formalmente, la probabilidad condicional de un suceso A dado que ha ocurrido un suceso B se define de la siguiente manera:

P(A | B) = P(A y B) / P(B)

Donde :

• P(A y B) es la probabilidad de que se produzcan los sucesos A y B, y
• P(B) es la probabilidad de que ocurra el suceso B.

La probabilidad condicional es importante en el trading y la inversión porque nos permite actualizar nuestras estimaciones de probabilidad a medida que disponemos de nueva información.

Por ejemplo, si sabemos que una empresa acaba de anunciar un informe de beneficios positivo, la probabilidad condicional de que el precio de la acción suba sobre la base de esta información es mayor que antes del anuncio.

Los inversores y los traders utilizan la probabilidad condicional para tomar decisiones mejor fundamentadas en función de la nueva información.

Al actualizar sus estimaciones de probabilidad, pueden evaluar mejor los riesgos y beneficios potenciales de una inversión determinada.

Esto puede ayudarles a realizar operaciones más rentables y a gestionar sus riesgos de forma más eficaz.

Por ejemplo, supongamos que un inversor está pensando en comprar una acción que siempre ha sido volátil.

Utilizando la probabilidad condicional, el inversor puede evaluar la probabilidad de que el precio de la acción suba o baje en función de diversas condiciones del mercado, como cambios en los tipos de interés, el crecimiento, la inflación, la política o los acontecimientos geopolíticos.

Esta información puede ayudar al inversor a tomar una decisión más informada sobre si comprar, mantener o vender la acción.

Ley de los grandes números

La ley de los grandes números es un concepto fundamental de la teoría de la probabilidad que describe el comportamiento de la media de un gran número de variables aleatorias independientes.

Esta ley establece que, a medida que aumenta el número de ensayos independientes, la media de estos ensayos converge al valor esperado de la distribución de probabilidad subyacente.

En términos más sencillos, la ley de los grandes números afirma que cuantas más veces se repita un experimento, más se acercarán los resultados observados al resultado esperado.

Ejemplo de lanzamiento de una moneda

Por ejemplo, si se lanza una moneda repetidamente, la ley de los grandes números predice que la frecuencia de caras se aproximará al 50% a medida que aumente el número de lanzamientos.

De 1.000 lanzamientos, es extremadamente improbable que una moneda justa salga 55/45 cara (0,17%), pero es bastante posible de 100 lanzamientos (36,8%).

Por qué es útil

La ley de los grandes números es útil en el trading y la inversión porque ayuda a mitigar el riesgo de fluctuaciones impredecibles del mercado.

Al invertir en una cartera diversificada, un inversor puede repartir su riesgo entre un gran número de activos, lo que puede ayudar a reducir el impacto de los movimientos de precios en activos individuales.

Además, la ley de los grandes números es útil para analizar los datos históricos del mercado y tomar decisiones de inversión con conocimiento de causa.

Al examinar un gran número de tendencias históricas del mercado, los inversores pueden ayudar a identificar patrones y tendencias que pueden ayudarles a tomar decisiones de inversión más informadas.

Por ejemplo, si un inversor quiere saber si la Reserva Federal ha bajado alguna vez los tipos de interés a pesar de una inflación por encima del objetivo, puede recurrir a la historia para ver si hay precedentes y el efecto que ha tenido en diversos mercados de activos.

Si existe una muestra, ¿de qué tamaño es para obtener suficientes datos útiles para determinar conclusiones útiles?

¿Qué relación existe entre la ley de los grandes números y la significación estadística?

La ley de los grandes números y la significación estadística son conceptos relacionados en estadística, pero no son idénticos.

La ley de los grandes números se refiere al hecho de que la media muestral de un gran número de observaciones independientes converge al valor esperado de la distribución de probabilidad subyacente a medida que el número de observaciones se aproxima al infinito.

Por otra parte, la significación estadística es una medida de la probabilidad de que los resultados observados en un estudio no se deban al azar.

En las pruebas estadísticas de hipótesis, un resultado se considera estadísticamente significativo si la probabilidad de obtener el resultado observado por azar está por debajo de un umbral predefinido, normalmente el 5% o menos.

En la práctica, la ley de los grandes números puede utilizarse para respaldar la significación estadística.

Cuando se recoge una muestra grande y la media de la muestra se aproxima al valor esperado de la distribución subyacente, esto sugiere que es menos probable que los resultados observados se deban al azar y más probable que sean estadísticamente significativos.

Sin embargo, es importante señalar que la significación estadística no implica necesariamente significación práctica o relevancia económica, y que la significación estadística por sí sola no debe utilizarse para tomar decisiones importantes.

Para tomar decisiones con conocimiento de causa, es esencial comprender bien los datos subyacentes, los métodos estadísticos y el contexto del problema estudiado.

Teorema de Bayes

El teorema de Bayes es un concepto fundamental de la teoría de la probabilidad que describe cómo actualizar las probabilidades a partir de nuevas pruebas o información.

Debe su nombre al reverendo Thomas Bayes, estadístico y teólogo británico del siglo XVIII.

El teorema permite calcular la probabilidad de una hipótesis o suceso a partir de los conocimientos o creencias previos (llamados probabilidad previa) y las nuevas pruebas (llamadas probabilidad).

La probabilidad actualizada se denomina probabilidad posterior y representa la probabilidad de la hipótesis o suceso tras tener en cuenta las nuevas pruebas.

La fórmula del teorema de Bayes es la siguiente

P(A|B) = P(B|A) * P(A) / P(B)

Donde :

• P(A|B) es la probabilidad posterior del suceso A dada la evidencia B
• P(B|A) es la probabilidad de la prueba B dado el suceso A
• P(A) es la probabilidad a priori del suceso A, y
• P(B) es la probabilidad de la prueba B

El teorema de Bayes es útil en el trading y la inversión porque puede ayudar a los inversores a actualizar sus creencias sobre la probabilidad de distintos sucesos en función de nueva información, como noticias sobre los beneficios de una empresa o indicadores económicos.

Y éste es un aspecto clave de la probabilidad bayesiana: actualiza sus creencias previas, sin necesidad de determinarlas o recalcularlas desde cero.

Utilizando el teorema de Bayes, los inversores pueden actualizar sus probabilidades y tomar decisiones de inversión más informadas.

Ejemplos de la importancia de comprobar nuestros supuestos

Cajero de banco

Un famoso ejemplo del teorema de Bayes en acción procede del estudio de Kahneman y Tversky.

En este estudio, los participantes recibieron la siguiente información:

Linda tiene 31 años, es soltera, franca y muy inteligente. Estudió filosofía. En su época de estudiante le preocupaban mucho la discriminación y la justicia social, y también participó en protestas antinucleares.

A continuación, se pide a los participantes que clasifiquen la probabilidad de dos escenarios posibles:

• Linda es cajera de banco.
• Linda es cajera de banco y participa activamente en el movimiento feminista.

A pesar de que el primer escenario incluye a más personas (todos los cajeros de banco) que el segundo (cajero de banco y feminista), muchos participantes clasificaron el segundo escenario como más probable.

Esto se debe a que la descripción de Linda se ajusta a su estereotipo de feminista, a pesar de que la probabilidad de que ocurran ambos sucesos es menor que la probabilidad de que ocurra el primero.

Este ejemplo demuestra la importancia de poner a prueba nuestros supuestos y tener en cuenta toda la información disponible antes de tomar decisiones.

El teorema de Bayes puede ayudar a los inversores a actualizar sus probabilidades y evitar sesgos que pueden conducir a decisiones incorrectas.

¿Steve es granjero o bibliotecario?

En el famoso estudio de Kahneman y Tversky se planteaba otra situación en la que se pedía a los participantes que determinaran la probabilidad de que Steve fuera agricultor o bibliotecario, basándose en información limitada sobre su personalidad.

Los participantes recibieron la siguiente información:

Steve es una persona callada y tímida a la que le gusta leer libros y no es muy sociable.

Basándose únicamente en esta información, la mayoría de los participantes concluyeron que era más probable que Steve fuera bibliotecario que agricultor. Sin embargo, Kahneman y Tversky demostraron que esta conclusión no estaba necesariamente justificada.

Para demostrarlo, presentaron a los participantes información adicional relevante pero no incluida en la descripción inicial.

Por ejemplo, añadieron información sobre el número de agricultores frente al de bibliotecarios y el porcentaje de agricultores con el tipo de personalidad de Steve, lo que seguía dando como resultado un mayor número de agricultores que el total de bibliotecarios.

Por ejemplo, si hay 20 veces más agricultores que bibliotecarios y el 20% de los agricultores se ajustan a este tipo de personalidad, sigue siendo 4 veces (20 * 0,20) más probable que Steve sea agricultor que bibliotecario.

Cuando los participantes recibieron esta nueva información, sus probabilidades de que Steve fuera agricultor aumentaron significativamente, lo que indica que sus conclusiones iniciales no estaban suficientemente fundamentadas.

Este estudio pone de relieve la importancia de comprobar los supuestos cuando se toman decisiones basadas en información limitada.

Es importante tener en cuenta todos los factores relevantes y no basarse únicamente en suposiciones o heurísticas iniciales, como los estereotipos, a la hora de tomar decisiones o emitir juicios.

Este planteamiento es coherente con el enfoque bayesiano de la probabilidad, que implica la actualización continua de las creencias en respuesta a la nueva información.

En el trading y la inversión, siempre es importante preguntarse cómo se sabe que se sabe.

Correlación y covarianza

Correlación y covarianza son dos conceptos estadísticos utilizados habitualmente en la teoría de la probabilidad para describir la relación entre dos variables aleatorias.

La covarianza mide el grado en que dos variables aleatorias se mueven juntas, mientras que la correlación mide la fuerza y la dirección de su relación.

Una covarianza positiva indica que las dos variables tienden a moverse en la misma dirección, mientras que una covarianza negativa indica que tienden a moverse en direcciones opuestas.

Un coeficiente de correlación oscila entre -1 y 1, con valores de 1 que indican una correlación positiva perfecta, valores de -1 que indican una correlación negativa perfecta y valores de 0 que indican ausencia de correlación.

En el trading y la inversión, la correlación y la covarianza son herramientas útiles para la gestión del riesgo y la diversificación de la cartera.

Al comprender la relación entre los distintos activos, los inversores pueden gestionar mejor sus carteras seleccionando activos que no estén muy correlacionados entre sí.

Esto puede ayudar a reducir el riesgo global de la cartera al repartir las inversiones entre diferentes clases de activos y sectores.

Por ejemplo, una cartera de acciones altamente correlacionadas puede ser más arriesgada que una cartera de acciones u otros activos poco correlacionados.

Seleccionando una gama diversificada de activos poco correlacionados, un inversor puede crear una cartera más resistente, con menos probabilidades de sufrir pérdidas significativas en un mercado bajista.

Además, comprender la correlación y la covarianza puede ayudar a los inversores a identificar pautas en el mercado y predecir tendencias futuras.

También es importante comprender que las correlaciones son retrospectivas y tienden a cambiar con el tiempo.

Por ejemplo, las acciones y los bonos pueden estar correlacionados negativamente en un entorno en el que los cambios en la inflación descontada disminuyen, pero pueden estar correlacionados positivamente en entornos en los que la inflación descontada aumenta.

Así pues, las interpretaciones más sólidas de la inflación examinarán más de cerca el estado intrínseco de los activos sobre la base de vínculos económicos causales, en lugar de interpretaciones retrospectivas como los simples coeficientes de correlación, que son sólo subproductos fugaces del entorno en el que se encuentran.

Brokers de CFDs

CFD Brokers	Plataformas	Regulado por la	Abrir una cuenta de demostración
	xStation 5	FCA, KNF, CySEC, BIFSC, CNMV, DFSA
	MetaTrader 4 y 5	CySEC, FCA, ASIC, JSC, OCRCVM, FSCA
	MetaTrader 4 y 5	ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM
ASIC: Australia, BaFin: Alemania, BIFSC: Belice, BVI FSC: Islas Vírgenes Británicas, BACEN & CVM: Brasil, CySEC: Chipre, CNMV: España, CMVM: Portugal, CSSF: Luxemburgo, CFTC: EE.UU., CBFSAI: Irlanda, CMA: Omán,, DFSA: Dubai, FCA: Reino Unido, FINMA: Suiza, FSPR - FMA: Nueva Zelanda, FRSA: Abu Dhabi, FSA: Seychelles, FSCA: Sudáfrica, JFSA: Japón, JSC: Jordania, KNF: Polonia, MAS: Singapur, OCRCVM: Canadá, SCB: Bahamas, VFSC: Vanuatu.
Las operaciones con CFDs implican un importante riesgo de pérdida, por lo que no son adecuadas para todos los inversores. Entre el 74 y el 89% de las cuentas de los inversores minoristas pierden dinero al operar con CFD.

FAQs - Teoría de la probabilidad en el trading

Conclusión - La teoría de la probabilidad en el trading

La teoría de la probabilidad desempeña un papel crucial en el trading, ya que ayuda a los operadores a tomar decisiones informadas basadas en el análisis de datos.

Gracias a la teoría de la probabilidad, los operadores pueden estimar la probabilidad de posibles movimientos del mercado y desarrollar estrategias de trading para sacar partido de dichos movimientos.

Ayuda a los traders a evaluar la relación riesgo-recompensa de una operación, gestionar su cartera y optimizar sus posiciones.

La teoría de la probabilidad es especialmente útil para cuantificar la incertidumbre y medir la volatilidad del mercado, lo que permite a los operadores anticiparse y prepararse para los cambios del mercado.

En general, la teoría de la probabilidad proporciona a los traders las herramientas para tomar decisiones de trading más informadas y precisas, lo que puede conducir a una mayor rentabilidad y a una reducción del riesgo.