Teoria della probabilità e trading

Cos'è la teoria delle probabilità e perché è importante?

La teoria delle probabilità è essenziale nel trading e negli investimenti perché consente agli operatori di mercato di comprendere e quantificare l'incertezza e il rischio associati alle decisioni finanziarie.

Come la vita stessa, anche il trading è una questione di probabilità. Raramente ci sono risultati ovvi, in bianco e nero, su cui è facile capitalizzare.

Utilizzando la teoria delle probabilità, i trader/investitori possono prendere decisioni più informate in base alla probabilità dei vari risultati.

Ecco alcuni motivi per cui la teoria delle probabilità è così importante nel trading/investimento:

Quantificare il rischio

La teoria delle probabilità consente agli investitori di calcolare la probabilità che si verifichino vari eventi, compresi gli scenari positivi e negativi.

Ciò consente ai trader di comprendere meglio i rischi potenziali associati alle diverse operazioni/investimenti.

Processo decisionale

La teoria delle probabilità consente ai trader di prendere decisioni migliori in base alla probabilità di diversi risultati e valutando le probabilità stesse (ciò che potrebbe essere chiamato "probabilità delle probabilità", in quanto le probabilità che le diverse cose accadano non sono note di per sé).

Ad esempio, se un investimento o una transazione ha il 70% di probabilità di produrre un rendimento positivo nell'arco di un anno, come si fa a saperlo?

La teoria delle probabilità copre aspetti come la varianza e come gestire meglio ciò che non si conosce e non si può conoscere.

Gestione del portafoglio

La teoria della probabilità aiuta i trader/investitori a gestire i loro portafogli fornendo un modo per valutare il rischio associato alle diverse classi di attività.

Analizzando la probabilità di risultati diversi, i trader/investitori possono creare un portafoglio diversificato che bilanci rischio e rendimento.

Gestione del rischio

La teoria delle probabilità è importante anche nella gestione del rischio, in quanto aiuta gli investitori a determinare la probabilità di eventi che potrebbero avere un impatto negativo sui loro investimenti/operazioni e ad adottare misure per mitigarli.

Nel complesso, la teoria delle probabilità è uno strumento importante per gli investitori/trader per comprendere i rischi e i benefici potenziali delle diverse opportunità di investimento, per fare scelte più informate e per ottenere migliori risultati a lungo termine.

In questo articolo esamineremo i diversi rami della teoria delle probabilità e le sue applicazioni nel trading.

Casualità

Nella teoria della probabilità, la casualità si riferisce al fatto che l'esito di un evento è imprevedibile e può variare da prova a prova.

Questo fenomeno viene spesso modellato utilizzando distribuzioni di probabilità, che descrivono la probabilità di ogni possibile risultato.

L'aleatorietà è un concetto fondamentale nella teoria della probabilità perché ci permette di quantificare ciò che non è noto e di fare previsioni sul futuro sulla base di informazioni incomplete.

In molte situazioni del mondo reale, gli esiti degli eventi sono influenzati da un gran numero di variabili difficili o impossibili da prevedere con certezza/precisione.

La casualità ci permette di tenerne conto e di stimare la probabilità di vari esiti sulla base di dati storici, causalità economica o altre informazioni.

Nel trading e negli investimenti, la casualità è sempre presente perché i mercati finanziari sono soggetti a un'ampia gamma di influenze.

Sui mercati operano molti tipi diversi di persone, di dimensioni diverse e con motivazioni diverse per il trading.

L'aleatorietà può manifestarsi sotto forma di volatilità del mercato, eventi inattesi o altri fattori che possono causare movimenti rapidi e imprevedibili dei prezzi.

Comprendere e tenere conto di questa casualità è essenziale per sviluppare strategie di trading di successo e gestire il rischio.

Più si acquisisce esperienza sui mercati, più ci si rende conto che tutto ciò che si sa impallidisce rispetto a ciò che si deve sapere in base a ciò che si realizza sui mercati.

Un modo in cui i trader e gli investitori possono affrontare la casualità è quello di utilizzare modelli basati sulle probabilità per prendere decisioni.

Ad esempio, un trader può utilizzare un modello statistico per stimare la probabilità di un aumento o di una diminuzione del prezzo di un particolare asset in un determinato periodo. Queste informazioni possono essere utilizzate per costruire un portafoglio ben bilanciato e gestire il rischio.

Ad esempio, se la distribuzione dei prezzi scontati di una particolare attività ha il seguente aspetto

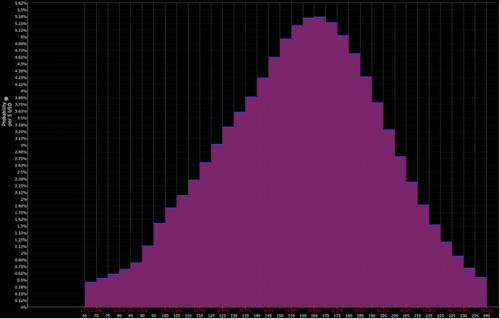
L'interpretazione del trader è più vicina alla combinazione delle distribuzioni rossa e viola (cioè un'inclinazione ribassista):

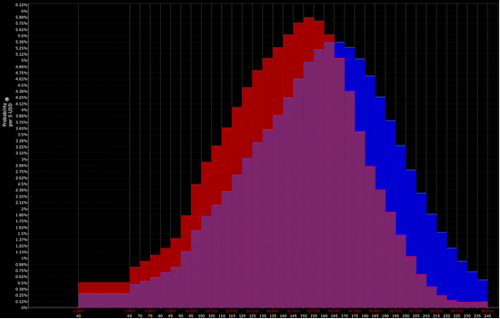
Si può quindi prevedere di assumere una posizione ribassista sull'asset. Poi, naturalmente, c'è la questione di come impostarla e delle dimensioni.

Esclusività reciproca

Nella teoria delle probabilità, il concetto di mutua esclusività si riferisce alla proprietà di due eventi diversi tra loro.

Matematicamente, due eventi A e B si dicono mutuamente esclusivi se la loro intersezione (cioè l'evento in cui si verificano sia A che B) è vuota, cioè P(A ∩ B) = 0.

L'esclusività reciproca è importante nel trading/investimento perché aiuta gli investitori a capire meglio come gestire i propri rischi.

Quando gli investitori detengono un portafoglio di attività, devono considerare le correlazioni tra le attività stesse.

Ad esempio, supponiamo che un trader/investitore abbia un portafoglio di azioni che comprende sia società tecnologiche che petrolifere. Se il prezzo del petrolio aumenta, le compagnie petrolifere possono trarne vantaggio, mentre i titoli tecnologici possono risentirne (ad esempio, a causa dell'effetto negativo dell'aumento del prezzo del petrolio sui tassi di interesse) e viceversa.

Tuttavia, se si verificano sviluppi in ciascun settore, questi potrebbero non influenzare i prezzi dei titoli dell'altro settore.

Pertanto, mentre i titoli sono correlati tra loro per alcuni aspetti - come le variazioni della crescita e dell'inflazione scontate - per altri aspetti si escludono a vicenda.

Come si separano questi fattori mutuamente esclusivi?

A volte si tratta semplicemente della natura del flusso finanziario - ad esempio, petrolio contro prodotti/servizi tecnologici.

A volte vengono chiamati fattori - ad esempio, momentum, dimensione, qualità, valore, ecc.

Inoltre, l'esclusività reciproca è importante nel trading di opzioni, dove il payoff di un'opzione può spesso basarsi sul mancato verificarsi di un altro evento. In questo contesto, l'esclusività reciproca aiuta i trader a coprire i rischi e a gestire l'esposizione.

Esperimento (prova di Bernoulli)

Un esperimento o prova di Bernoulli è un concetto fondamentale della teoria della probabilità che si riferisce a un evento casuale con due soli esiti possibili.

Ad esempio, il lancio di una moneta è un esperimento di Bernoulli, in cui i risultati possibili sono testa o croce.

Un altro esempio è la possibilità che una particolare operazione in opzioni sia redditizia (in-the-money) o meno (out-of-the-money) alla scadenza.

Nella teoria delle probabilità, la probabilità di successo (cioè il risultato di interesse) è definita da p, mentre la probabilità di fallimento (cioè il risultato alternativo) è definita da q = 1 - p.

Gli esiti di un processo di Bernoulli sono spesso indicati con 1 per il successo e 0 per il fallimento.

L'importanza dei processi di Bernoulli nel trading e negli investimenti è data dal fatto che alcune decisioni finanziarie comportano esiti binari.

Ad esempio, si può decidere di acquistare un'opzione azionaria nella speranza che vada in pareggio, oppure di venderla nella speranza che il suo prezzo vada in pareggio e che si riceva l'intero premio.

In entrambi i casi, il risultato è binario in termini di denaro. Le scommesse binarie pure assumono la forma di opzioni binarie.

Applicando i principi della teoria delle probabilità al trading e agli investimenti, è possibile prendere decisioni più consapevoli su quando acquistare o vendere.

Esistono anche concetti come il valore atteso, che insegnano a non puntare sempre sul risultato più probabile.

Distribuzione di probabilità

Nella teoria delle probabilità, una distribuzione di probabilità è una funzione che descrive la probabilità di diversi risultati in un esperimento o processo casuale.

Specifica le probabilità di tutti i possibili esiti di un evento e la somma delle probabilità di tutti gli esiti è uguale a uno.

Esistono molti tipi di distribuzioni di probabilità, ma le più comuni sono la distribuzione normale, la distribuzione binomiale e la distribuzione di Poisson.

Ogni distribuzione ha un proprio insieme di parametri che ne determinano la forma, e questi parametri sono spesso utilizzati per fare previsioni e prendere decisioni.

Naturalmente, nei mercati finanziari i rendimenti tendono ad avere code più larghe e non si adattano a una distribuzione predeterminata, quindi tendono a essere personalizzati.

In generale, le distribuzioni di probabilità sono importanti perché forniscono un quadro di riferimento per comprendere il rischio e l'incertezza associati agli investimenti finanziari.

Uno dei concetti più importanti nel trading/investimento è che tutto è una probabilità (cioè una distribuzione di risultati potenziali). Non esiste un singolo risultato particolarmente probabile.

Utilizzando le distribuzioni di probabilità, trader e investitori possono stimare la probabilità di risultati diversi e prendere decisioni più informate su come allocare le proprie risorse.

Ad esempio, un trader potrebbe utilizzare la distribuzione normale o una distribuzione a coda grossa per modellare i rendimenti giornalieri di un particolare titolo.

Potrebbe quindi utilizzare questa distribuzione per stimare la probabilità che il rendimento del titolo superi una certa soglia, ad esempio un rendimento del +/-5% in un giorno.

Utilizzando le distribuzioni di probabilità in questo modo, i trader possono gestire meglio il rischio e ottimizzare i rendimenti.

Oltre a stimare le probabilità, le distribuzioni di probabilità vengono utilizzate anche per creare strumenti finanziari come le opzioni e i futures.

Questi strumenti sono prezzati in base alla distribuzione sottostante dell'attività a cui sono collegati e i trader possono utilizzarli per coprire il rischio o fare scommesse sui futuri movimenti di prezzo dell'attività.

Inoltre, le distribuzioni possono essere costruite sulla base del prezzo delle opzioni sottostanti, come illustrato di seguito.

Distribuzione scontata dai mercati :

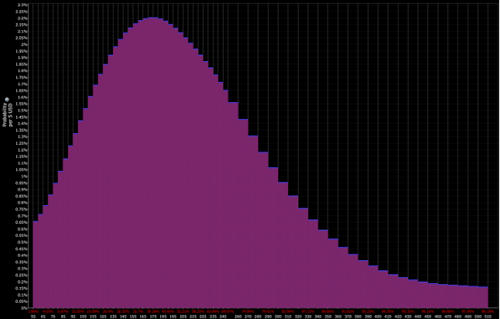
Distribuzione determinata dal trader (che apre le porte a opportunità tattiche):

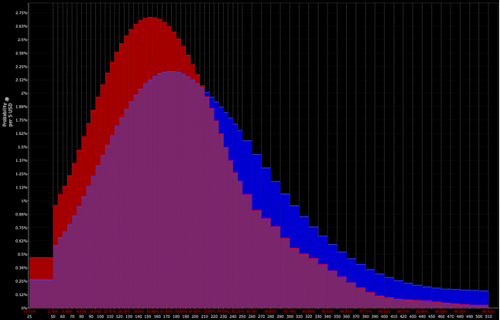
Distribuzione binomiale

La distribuzione binomiale è una distribuzione di probabilità che modella il numero di esiti positivi in una serie di prove indipendenti e identiche, in cui ogni prova ha solo due esiti possibili (ad esempio, testa o croce, vincere o perdere, alto o basso).

I parametri chiave della distribuzione binomiale sono la probabilità di successo in una singola prova (indicata con p) e il numero di prove (indicato con n).

La distribuzione binomiale è importante nel campo del trading e degli investimenti perché può essere utilizzata per modellare la distribuzione dei rendimenti di una strategia di trading binario (ad esempio, una strategia che prevede l'acquisto o la vendita di un'attività a seconda che si verifichi un determinato evento).

In particolare, il valore atteso di una strategia di trading binario può essere calcolato utilizzando la distribuzione binomiale.

Il valore atteso di una strategia di trading binario è la somma dei prodotti della probabilità di ogni possibile risultato e del rendimento di tale risultato.

Per esempio, se una strategia di trading binario ha una probabilità del 60% di ottenere un rendimento del 10% e una probabilità del 40% di ottenere un rendimento del -5%, il valore atteso della strategia è

(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04

La distribuzione binomiale può essere utilizzata per calcolare le probabilità di ogni possibile risultato in una serie di operazioni binarie.

Ad esempio, se un trader effettua 10 operazioni binarie con una probabilità di successo del 60% e una probabilità di insuccesso del 40%, la probabilità di effettuare un certo numero di operazioni di successo (cioè una certa percentuale di successo) può essere calcolata utilizzando la distribuzione binomiale.

Questo può aiutare il trader a valutare il rischio e il potenziale rendimento della sua strategia di trading.

Valore atteso

Abbiamo parlato del valore atteso (VA) in altri articoli, in quanto si tratta di un concetto fondamentale della teoria della probabilità che descrive il risultato medio di una variabile casuale.

Nel campo del trading e degli investimenti, il valore atteso viene utilizzato per calcolare il rendimento potenziale e il rischio di un investimento o di una strategia di trading.

Matematicamente, il valore atteso di una variabile casuale è la somma dei prodotti di ogni possibile risultato e della sua probabilità.

Ad esempio, si consideri il lancio di una moneta che dà come risultato 1 dollaro per la testa e 0 dollari per la croce.

Il valore atteso di questo lancio di moneta è il seguente:

VA = (0,5 * 1$) + (0,5 * 0$) = 0,50$.

Ciò significa che il payoff medio per il lancio di questa moneta è di 0,50 dollari. In questo modo si raggiunge un punto di pareggio nel tempo, poiché le probabilità corrispondono a quelle reali.

Nel trading e negli investimenti, il valore atteso viene utilizzato per stimare i rendimenti potenziali di una strategia di trading o di un investimento.

Ad esempio, se un'azione ha il 60% di probabilità di aumentare di valore del 10% e il 40% di diminuire di valore del 5%, il rendimento atteso dell'investimento può essere calcolato come segue:

VA = (0,6 * 10%) + (0,4 * -5%) = 6% - 2% = 4%

Ciò significa che il rendimento atteso dell'investimento è del 4%.

Queste informazioni possono aiutare gli investitori e i trader a decidere di investire in un'azione e a valutare il rischio e il potenziale rendimento del loro investimento.

Il valore atteso è importante anche nella gestione del rischio.

Calcolando il valore atteso di una strategia di trading o di un investimento, trader e investitori possono valutare il rischio potenziale dell'investimento.

Ad esempio, se il valore atteso di un investimento è negativo, significa che è probabile che l'investimento perda denaro in media nel lungo periodo.

I trader/investitori possono utilizzare queste informazioni per gestire il rischio diversificando gli investimenti o limitando l'esposizione all'investimento o alla transazione.

Inoltre, come abbiamo discusso in altri articoli, puntare sul risultato con il valore atteso più alto non è sempre la decisione migliore.

A volte è meglio avere un valore atteso più basso, se ciò consente di ottenere una varianza inferiore (minor rischio di perdita o fallimento). Inoltre, bisogna sempre assicurarsi di poter coprire le perdite.

Ad esempio, se avete 1.000 dollari e avete il 90% di possibilità di raddoppiare il vostro denaro fino a 2.000 dollari e il 10% di perdere tutti i 1.000 dollari, il vostro EV è molto alto (1.800 dollari - 1.000 dollari = +800 dollari).

Ma se non potete permettervi di perdere i 1.000 dollari in caso di errore, è meglio non prendere la decisione.

Catena di Markov

La catena di Markov è un concetto matematico della teoria della probabilità che descrive un processo in cui il passo o lo stato successivo dipende solo dallo stato attuale e non dagli stati precedenti.

In altre parole, si tratta di un processo privo di memoria che si basa solo sullo stato corrente per determinare lo stato futuro.

Una catena di Markov è definita da un insieme di stati e dalle probabilità di passare da uno stato all'altro.

Queste probabilità sono spesso rappresentate in una matrice di transizione, dove ogni elemento della matrice rappresenta la probabilità di passare da uno stato all'altro.

La catena di Markov è importante nel campo del trading/investimento perché può essere utilizzata per modellare il comportamento dei mercati finanziari.

Il mercato azionario, ad esempio, è un sistema complesso con un gran numero di variabili che influenzano il prezzo dei titoli che lo compongono.

La catena di Markov consente di semplificare il sistema, concentrandosi solo sullo stato attuale del mercato e sulle probabilità di passare ad altri stati.

Modellando il mercato azionario come una catena di Markov, i trader e gli investitori possono potenzialmente ottenere ulteriori informazioni prevedendo i futuri movimenti del mercato sulla base dello stato attuale.

La catena di Markov può anche essere utilizzata per calcolare varie misure come i rendimenti attesi, la volatilità e il rischio.

Inoltre, la catena di Markov viene utilizzata in varie tecniche di modellazione finanziaria, come il pricing delle opzioni, l'ottimizzazione del portafoglio e la gestione del rischio.

Consente ai trader/investitori di creare e testare diverse strategie di investimento e di misurarne l'efficacia in diverse condizioni di mercato.

Cammino casuale

Il cammino casuale è un concetto matematico della teoria della probabilità che descrive il movimento di un oggetto in modo casuale e imprevedibile.

In una passeggiata casuale, la posizione successiva dell'oggetto è determinata da un processo casuale, come il lancio di una moneta o di un dado.

In finanza, un modello di random walk viene spesso utilizzato per descrivere l'evoluzione dei prezzi delle azioni nel tempo.

La teoria alla base di questo modello è che il movimento dei prezzi delle azioni è imprevedibile e segue un andamento casuale.

Ciò significa che il prezzo di un'azione in un determinato momento ha la stessa probabilità di salire o scendere e che il movimento del prezzo dell'azione nel tempo non è influenzato dai prezzi passati o da altri fattori esterni. (Naturalmente esistono varie idee e teorie su trend, momentum, ecc.).

Il concetto di random walk è utile da conoscere nel trading e negli investimenti perché suggerisce che è molto difficile prevedere l'andamento dei prezzi delle azioni.

Ciò significa che è difficile battere il mercato acquistando e vendendo azioni in base ai movimenti di prezzo passati o ad altre informazioni.

Gli investitori e i trader possono utilizzare il concetto di random walk per supportare la loro strategia di investimento e prendere decisioni più informate.

Ad esempio, possono scegliere di investire in un portafoglio diversificato di azioni per ridurre l'esposizione ai movimenti dei prezzi dei singoli titoli e diversificare per attività, classi di attività, Paesi e valute, e considerare l'utilizzo di una strategia buy-and-hold per evitare i costi e i rischi del trading frequente.

Processo stocastico

Il processo stocastico è un quadro matematico utilizzato per modellare il comportamento di un sistema che si evolve in modo casuale nel tempo.

Si tratta di un insieme di variabili casuali indicizzate dal tempo, il che significa che il valore del processo in un dato momento è casuale.

I processi stocastici sono utili nella teoria della probabilità perché ci aiutano ad analizzare il comportamento di fenomeni casuali che si evolvono nel tempo.

Forniscono un modo per modellare e comprendere la casualità di questi fenomeni, che possono essere utilizzati per fare previsioni e prendere decisioni basate sui risultati attesi.

Nel campo del trading e degli investimenti, i processi stocastici sono utilizzati per modellare alcuni comportamenti dei mercati finanziari e dei prezzi delle attività.

Essi consentono di analizzare la casualità e la volatilità dei dati finanziari, che possono essere utilizzati per prendere decisioni su quando acquistare o vendere attività.

Ad esempio, i processi stocastici possono essere utilizzati per modellare il movimento dei prezzi delle azioni o dei tassi di cambio, aiutando così i trader e gli investitori a fare previsioni sui movimenti futuri di questi mercati.

I processi stocastici sono utilizzati anche per sviluppare e testare strategie di trading. Simulando il comportamento dei mercati finanziari con processi stocastici, i trader e gli investitori possono testare le loro strategie di trading e valutarne le prestazioni in diverse condizioni di mercato.

Probabilità condizionata

La probabilità condizionata è un concetto fondamentale della teoria della probabilità che si riferisce alla probabilità che un evento si verifichi se un altro evento si è già verificato. È un modo per aggiornare le nostre stime di probabilità sulla base di nuove informazioni.

Più formalmente, la probabilità condizionata di un evento A dato che si è verificato un evento B è definita come segue:

P(A | B) = P(A e B) / P(B)

Dove :

• P(A e B) è la probabilità che si verifichino entrambi gli eventi A e B, e
• P(B) è la probabilità che si verifichi l'evento B.

La probabilità condizionata è importante nel trading e negli investimenti perché ci permette di aggiornare le nostre stime di probabilità quando sono disponibili nuove informazioni.

Ad esempio, se sappiamo che una società ha appena annunciato un bilancio positivo, la probabilità condizionata che il prezzo delle azioni salga in base a questa informazione è più alta rispetto a prima dell'annuncio.

Gli investitori e i trader utilizzano la probabilità condizionata per prendere decisioni più informate sulla base di nuove informazioni.

Aggiornando le loro stime di probabilità, possono valutare meglio i rischi e i benefici potenziali di un determinato investimento.

Questo può aiutarli a fare operazioni più redditizie e a gestire i rischi in modo più efficace.

Ad esempio, supponiamo che un investitore stia pensando di acquistare un titolo che è sempre stato volatile.

Utilizzando la probabilità condizionata, l'investitore può valutare la probabilità che il prezzo dell'azione aumenti o diminuisca in base a varie condizioni di mercato, come le variazioni dei tassi di interesse, la crescita, l'inflazione, la politica o gli eventi geopolitici.

Queste informazioni possono aiutare l'investitore a prendere una decisione più informata sull'acquisto, la detenzione o la vendita del titolo.

Legge dei grandi numeri

La legge dei grandi numeri è un concetto fondamentale della teoria della probabilità che descrive il comportamento della media di un gran numero di variabili casuali indipendenti.

Questa legge afferma che all'aumentare del numero di prove indipendenti, la media di queste prove converge al valore atteso della distribuzione di probabilità sottostante.

In termini più semplici, la legge dei grandi numeri afferma che più volte viene ripetuto un esperimento, più i risultati osservati si avvicinano al risultato atteso.

Esempio di lancio di una moneta

Ad esempio, lanciando ripetutamente una moneta, la legge dei grandi numeri prevede che la frequenza di testa si avvicini al 50% con l'aumentare del numero di lanci.

Su 1.000 lanci, è estremamente improbabile che una moneta giusta esca 55/45 in entrambi i casi (0,17%), ma è abbastanza possibile su 100 lanci (36,8%).

Perché è utile

La legge dei grandi numeri è utile nel trading e negli investimenti perché aiuta a mitigare il rischio di fluttuazioni imprevedibili del mercato.

Investendo in un portafoglio diversificato, un investitore può distribuire il proprio rischio su un gran numero di attività, il che può contribuire a ridurre l'impatto dei movimenti di prezzo delle singole attività.

Inoltre, la legge dei grandi numeri è utile per analizzare i dati storici del mercato e prendere decisioni di investimento informate.

Esaminando un gran numero di andamenti storici del mercato, gli investitori possono identificare modelli e tendenze che possono aiutarli a prendere decisioni di investimento più informate.

Ad esempio, se un trader vuole sapere se la Federal Reserve ha mai tagliato i tassi di interesse nonostante un'inflazione superiore all'obiettivo, può guardare alla storia per vedere se ci sono precedenti e l'effetto che ha avuto sui vari mercati degli asset.

Se esiste un campione, quanto è grande per ottenere un numero di dati sufficienti a determinare conclusioni utili?

Che rapporto c'è tra la legge dei grandi numeri e la significatività statistica?

La legge dei grandi numeri e la significatività statistica sono concetti correlati in statistica, ma non sono identici.

La legge dei grandi numeri si riferisce al fatto che la media campionaria di un gran numero di osservazioni indipendenti converge al valore atteso della distribuzione di probabilità sottostante man mano che il numero di osservazioni si avvicina all'infinito.

La significatività statistica, invece, è una misura della probabilità che i risultati osservati di uno studio non siano dovuti al caso.

Nei test di ipotesi statistica, un risultato è considerato statisticamente significativo se la probabilità di ottenere il risultato osservato per caso è inferiore a una soglia predefinita, di solito il 5% o meno.

In pratica, la legge dei grandi numeri può essere utilizzata a sostegno della significatività statistica.

Quando viene raccolto un campione ampio e la media del campione è vicina al valore atteso della distribuzione sottostante, ciò suggerisce che i risultati osservati hanno meno probabilità di essere dovuti al caso e più probabilità di essere statisticamente significativi.

Tuttavia, è importante notare che la significatività statistica non implica necessariamente una rilevanza pratica o economica e che la significatività statistica da sola non dovrebbe essere utilizzata per prendere decisioni importanti.

Per prendere decisioni informate, è essenziale avere una buona comprensione dei dati sottostanti, dei metodi statistici e del contesto del problema da studiare.

Teorema di Bayes

Il teorema di Bayes è un concetto fondamentale della teoria della probabilità che descrive come aggiornare le probabilità in base a nuove prove o informazioni.

Prende il nome dal reverendo Thomas Bayes, statistico e teologo britannico del XVIII secolo.

Il teorema fornisce un modo per calcolare la probabilità di un'ipotesi o di un evento in base alle conoscenze o alle credenze precedenti (chiamate probabilità anteriore) e alle nuove prove (chiamate probabilità).

La probabilità aggiornata è chiamata probabilità posteriore e rappresenta la probabilità dell'ipotesi o dell'evento dopo aver tenuto conto delle nuove prove.

La formula del teorema di Bayes è la seguente:

P(A|B) = P(B|A) * P(A) / P(B)

Dove :

• P(A|B) è la probabilità posteriore dell'evento A data l'evidenza B
• P(B|A) è la probabilità della prova B dato l'evento A
• P(A) è la probabilità anteriore dell'evento A e
• P(B) è la probabilità della prova B

Il teorema di Bayes è utile nel trading e negli investimenti perché può aiutare gli investitori ad aggiornare le loro convinzioni sulla probabilità di eventi diversi in base a nuove informazioni, come le notizie sugli utili di una società o gli indicatori economici.

Questo è un aspetto chiave della probabilità bayesiana: aggiorna le credenze preliminari, senza necessariamente determinarle o ricalcolarle da zero.

Utilizzando il teorema di Bayes, gli investitori possono aggiornare le loro probabilità e prendere decisioni di investimento più informate.

Esempi dell'importanza di verificare le nostre ipotesi

Cassiere di banca

Un famoso esempio del teorema di Bayes in azione viene dallo studio di Kahneman e Tversky.

In questo studio, ai partecipanti sono state fornite le seguenti informazioni:

Linda ha 31 anni, è single, schietta e molto intelligente. Ha studiato filosofia. Da studentessa era molto preoccupata per le discriminazioni e le questioni di giustizia sociale, e ha anche partecipato a proteste antinucleari.

Ai partecipanti è stato chiesto di classificare la probabilità di due possibili scenari:

• Linda è una cassiera di banca.
• Linda è una cassiera di banca ed è attiva nel movimento femminista.

Nonostante il fatto che il primo scenario includa più persone (tutti i cassieri di banca) rispetto al secondo (cassiere di banca e femminista), molti partecipanti hanno classificato il secondo scenario come più probabile.

Questo perché la descrizione di Linda corrisponde al loro stereotipo di femminista, anche se la probabilità che entrambi gli eventi si verifichino è inferiore alla probabilità del primo evento.

Questo esempio dimostra l'importanza di verificare le nostre ipotesi e di prendere in considerazione tutte le informazioni disponibili prima di prendere decisioni.

Il teorema di Bayes può aiutare gli investitori ad aggiornare le proprie probabilità e a evitare pregiudizi che possono portare a decisioni errate.

Steve è un contadino o un bibliotecario?

Il famoso studio condotto da Kahneman e Tversky prevedeva un altro scenario in cui i partecipanti dovevano determinare la probabilità che Steve fosse un contadino o un bibliotecario, sulla base di informazioni limitate sulla sua personalità.

I partecipanti hanno ricevuto le seguenti informazioni:

Steve è un individuo tranquillo e timido a cui piace leggere libri e non è molto socievole.

Basandosi solo su queste informazioni, la maggior parte dei partecipanti ha concluso che Steve era più probabile che fosse un bibliotecario piuttosto che un agricoltore. Tuttavia, Kahneman e Tversky hanno mostrato che questa conclusione non era necessariamente giustificata.

Per dimostrarlo, hanno presentato ai partecipanti informazioni aggiuntive che erano rilevanti ma non incluse nella descrizione iniziale.

Ad esempio, hanno aggiunto informazioni sul numero di agricoltori contro bibliotecari e sulla percentuale di agricoltori con il tipo di personalità di Steve, che ha comunque fornito un numero di agricoltori superiore al numero totale di bibliotecari.

Ad esempio, se ci sono 20 volte più agricoltori che bibliotecari e il 20% degli agricoltori corrisponde a questo tipo di personalità, è ancora 4 volte (20 * 0,20) più probabile che Steve sia un contadino piuttosto che un bibliotecario.

Quando i partecipanti hanno ricevuto queste nuove informazioni, le loro probabilità che Steve fosse un agricoltore sono aumentate in modo significativo, indicando che le loro conclusioni iniziali non erano sufficientemente informate.

Questo studio sottolinea l'importanza di verificare le ipotesi quando si prendono decisioni basate su informazioni limitate.

È importante considerare tutti i fattori rilevanti e non fare affidamento esclusivamente su presupposti iniziali o euristiche, come gli stereotipi, quando si prendono decisioni o si formulano giudizi.

Questo approccio è coerente con l'approccio bayesiano alla probabilità, che comporta l'aggiornamento continuo delle convinzioni basate su nuove informazioni.

Nel trading e negli investimenti, è sempre importante chiedersi come fai a sapere di saperlo?

Correlazione e covarianza

La correlazione e la covarianza sono due concetti statistici comunemente utilizzati nella teoria della probabilità per descrivere la relazione tra due variabili casuali.

La covarianza misura la misura in cui due variabili casuali si muovono insieme, mentre la correlazione misura la forza e la direzione della loro relazione.

Una covarianza positiva indica che le due variabili tendono a muoversi nella stessa direzione, mentre una covarianza negativa indica che tendono a muoversi in direzioni opposte.

Il coefficiente di correlazione varia da -1 a 1, con valori di 1 che indicano una perfetta correlazione positiva, valori di -1 che indicano una perfetta correlazione negativa e valori di 0 che indicano l'assenza di correlazione.

Nel trading/investimento, la correlazione e la covarianza sono strumenti utili per la gestione del rischio e la diversificazione del portafoglio.

Comprendendo la relazione tra le diverse attività, gli investitori possono gestire meglio i loro portafogli selezionando attività che non sono altamente correlate tra loro.

Ciò può contribuire a ridurre il rischio complessivo del portafoglio, distribuendo gli investimenti su diverse classi di attività e settori.

Ad esempio, un portafoglio di titoli azionari altamente correlati può essere più rischioso di un portafoglio di titoli azionari o altri asset poco correlati.

Selezionando una gamma diversificata di attività a bassa correlazione, l'investitore può creare un portafoglio più resistente che ha meno probabilità di subire perdite significative in un mercato in ribasso.

Inoltre, la comprensione della correlazione e della covarianza può aiutare gli investitori a identificare i modelli del mercato e a prevedere le tendenze future.

È anche importante capire che le correlazioni sono retrospettive e tendono a cambiare nel tempo.

Ad esempio, le azioni e le obbligazioni possono essere correlate negativamente in un ambiente in cui le variazioni dell'inflazione attualizzata sono in diminuzione, ma possono essere correlate positivamente in ambienti in cui l'inflazione attualizzata è in aumento.

Pertanto, interpretazioni più solide dell'inflazione esamineranno più da vicino lo stato intrinseco degli asset sulla base di legami economici causali, piuttosto che interpretazioni retrospettive come i semplici coefficienti di correlazione, che sono solo sottoprodotti fugaci dell'ambiente in cui si trovano.

Broker di CFD

CFD Brokers	Piattaforma	Regolazione	Aprire un conto demo
	MetaTrader 4 e 5 AvaOptions	ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM
	MetaTrader 4 e 5 cTrader, TradingView	FCA, ASIC, CySEC, BaFin, DFSA, SCB, CMA
	xStation 5	FCA, KNF, CySEC, BIFSC, CNMV, DFSA
	MetaTrader 4 e 5	CySEC, FCA, ASIC, JSC, OCRCVM, FSCA
	MetaTrader 4 e 5 ActivTrader, TradingView	FCA, CSSF, SCB, BACEN & CVM, CMVM
	MetaTrader 4 y 5 ActivTrader, TradingView	FCA, BaFin, ASIC, FINMA, FSCA, MAS, FMA, DFSA, JFSA, CFTC
	MetaTrader 4 e 5	CySEC,ASIC,BIFSC
ASIC: Australia, BaFin: Germania, BIFSC: Belize, BVI FSC: Isole Vergini britanniche, BACEN e CVM: Brasile, CySEC: Cipro, CNMV: Spagna, CMVM: Portogallo, CSSF: Lussemburgo, CFTC: USA, CBFSAI: Irlanda, CMA : Oman, DFSA: Dubai, FCA: Regno Unito, FINMA: Svizzera, FSPR - FMA: Nuova Zelanda, FRSA: Abu Dhabi, FSA: Seychelles, FSCA: Sud Africa, JFSA: Giappone, JSC: Giordania, KNF: Polonia , MAS: Singapore, IIROC: Canada, SCB: Bahamas, VFSC: Vanuatu
Il trading di CFD comporta un significativo rischio di perdita, quindi non è adatto a tutti gli investitori. Il 74-89% dei conti degli investitori al dettaglio perde denaro nel trading di CFD.

FAQ - La teoria delle probabilità nel trading

Conclusione - La teoria delle probabilità nel trading

La teoria delle probabilità svolge un ruolo cruciale nel trading, in quanto aiuta i trader a prendere decisioni informate sulla base di analisi basate sui dati.

Utilizzando la teoria delle probabilità, i trader possono stimare la probabilità di potenziali movimenti di mercato e sviluppare strategie di trading per capitalizzare questi movimenti.

Aiuta i trader a valutare il rapporto rischio-rendimento di un'operazione, a gestire il portafoglio e a ottimizzare le posizioni.

La teoria delle probabilità è particolarmente utile per quantificare l'incertezza e misurare la volatilità del mercato, consentendo ai trader di anticipare e prepararsi ai cambiamenti del mercato.

Nel complesso, la teoria delle probabilità fornisce ai trader gli strumenti per prendere decisioni di trading più informate e accurate, che possono portare a una maggiore redditività e a una riduzione del rischio.