Sannolikhetsteori och handel
Vad är sannolikhetsteori och varför är den viktig?

Sannolikhetsteorin är viktig för handel och investeringar eftersom den gör det möjligt för marknadsaktörerna att förstå och kvantifiera osäkerheten och risken i samband med finansiella beslut.
Precis som livet i sig handlar handel om sannolikheter. Det finns sällan uppenbara, svartvita resultat som är lätta att dra nytta av.
Genom att använda sannolikhetsteorin kan handlare/investerare fatta mer välgrundade beslut utifrån sannolikheten för olika utfall.
Här är några anledningar till varför sannolikhetsteori är så viktig inom handel/investeringar:
Kvantifiering av risker
Sannolikhetsteorin gör det möjligt för investerare att beräkna sannolikheten för att olika saker händer, inklusive positiva och negativa scenarier.
Detta gör det möjligt för handlare att bättre förstå de potentiella risker som är förknippade med olika affärer/investeringar.
Beslutsfattande
Sannolikhetsteorin gör det möjligt för näringsidkare att fatta bättre beslut utifrån sannolikheten för olika utfall och genom att bedöma sannolikheterna själva (det som skulle kunna kallas "sannolikhet av sannolikheter", eftersom sannolikheten för att olika saker ska inträffa inte är känd i sig).
Om en investering eller transaktion till exempel har 70 procents sannolikhet att ge en positiv avkastning under ett år, hur vet du det?
Sannolikhetsteorin omfattar saker som varians och hur man bättre kan hantera det man inte vet och inte kan veta.
Förvaltning av portföljer
Sannolikhetsteorin hjälper handlare/investerare att förvalta sina portföljer genom att tillhandahålla ett sätt att bedöma den risk som är förknippad med olika tillgångsklasser.
Genom att analysera sannolikheten för olika utfall kan handlare/investerare skapa en diversifierad portfölj som balanserar risk och avkastning.
Riskhantering
Sannolikhetsteorin är också viktig inom riskhantering, eftersom den hjälper investerare att fastställa sannolikheten för händelser som skulle kunna påverka deras investeringar/verksamhet negativt och vidta åtgärder för att mildra dem.
Sammantaget är sannolikhetsteorin ett viktigt verktyg för investerare/handlare för att förstå de potentiella riskerna och vinsterna med olika investeringsmöjligheter, för att göra mer välgrundade val och uppnå bättre långsiktiga resultat.
I den här artikeln kommer vi att titta på sannolikhetsteorins olika grenar och dess tillämpningar inom handel.
Slumpmässighet
Inom sannolikhetsteorin avser slumpmässighet det faktum att resultatet av en händelse är oförutsägbart och kan variera från försök till försök.
Detta fenomen modelleras ofta med hjälp av sannolikhetsfördelningar, som beskriver sannolikheten för varje möjligt resultat.
Slumpmässighet är ett grundläggande begrepp i sannolikhetsteorin eftersom det gör det möjligt för oss att kvantifiera det som är okänt och att göra förutsägelser om framtiden på grundval av ofullständig information.
I många situationer i den verkliga världen påverkas utfallet av ett stort antal variabler som är svåra eller omöjliga att förutsäga med säkerhet/precision.
Slumpmässigheten gör det möjligt för oss att ta hänsyn till detta och uppskatta sannolikheten för olika utfall på grundval av historiska data, ekonomisk kausalitet eller annan information.
Vid handel och investeringar är slumpmässighet alltid närvarande eftersom de finansiella marknaderna är föremål för ett stort antal influenser.
Det finns många olika typer av människor på marknaderna, av olika storlek och med olika motiv för handel.
Slumpmässigheten kan visa sig i form av marknadsvolatilitet, oväntade händelser eller andra faktorer som kan orsaka snabba och oförutsägbara prisrörelser.
Att förstå och ta hänsyn till denna slumpmässighet är viktigt för att utveckla framgångsrika handelsstrategier och hantera risker.
Ju mer erfarenhet människor får på marknaderna, desto mer inser de att allt de vet bleknar i jämförelse med de saker de behöver veta utifrån vad som aktualiseras på marknaderna.
Ett sätt för handlare och investerare att hantera slumpmässighet är att använda sannolikhetsbaserade modeller för att fatta beslut.
En näringsidkare kan till exempel använda en statistisk modell för att uppskatta sannolikheten för en ökning eller minskning av priset på en viss tillgång under en viss period. Denna information kan sedan användas för att bygga en välbalanserad portfölj och hantera risken.
Om fördelningen av diskonterade priser för en viss tillgång till exempel ser ut så här
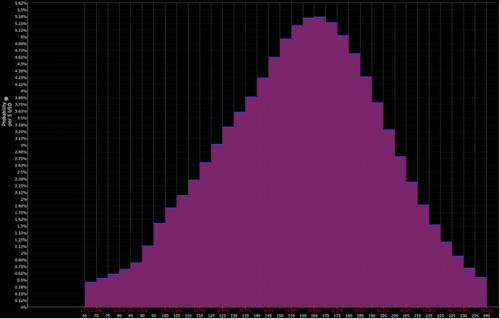
Och näringsidkarens tolkning ligger närmare kombinationen av den röda och lila fördelningen (dvs. en nedåtgående tendens):
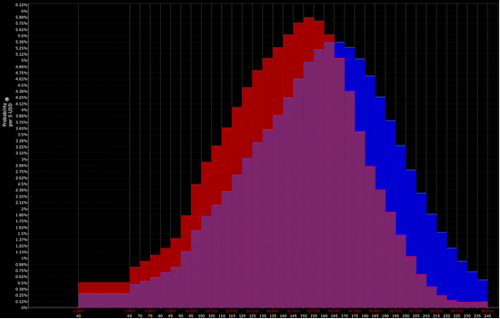
De kan då förvänta sig att inta en björnposition i tillgången. Sedan är det naturligtvis frågan om hur den ska läggas upp och hur stor den ska vara.
Ömsesidig exklusivitet
Inom sannolikhetsteorin hänvisar begreppet ömsesidig exklusivitet till egenskapen att två händelser är olika från varandra.
Matematiskt sett sägs två händelser A och B vara ömsesidigt uteslutande om deras skärningspunkt (dvs. den händelse där både A och B inträffar) är tom, dvs. P(A ∩ B) = 0.
Ömsesidig exklusivitet är viktigt inom handel/investeringar eftersom det hjälper investerare att bättre förstå hur de ska hantera sina risker.
När investerare har en portfölj av tillgångar måste de ta hänsyn till korrelationerna mellan/bland deras tillgångar.
Låt oss till exempel säga att en näringsidkare/investerare har en aktieportfölj som innehåller både teknik- och oljebolag. Om oljepriset stiger kan detta hjälpa oljebolagen, men teknikaktierna kan drabbas (t.ex. på grund av den negativa effekten av stigande oljepriser på räntorna), och vice versa.
Om det sker en utveckling i varje sektor kan det dock hända att den inte påverkar priserna på aktierna i den andra sektorn.
Även om värdepapper är relaterade till varandra i vissa avseenden - t.ex. förändringar i diskonterad tillväxt och inflation - är de alltså ömsesidigt uteslutande i andra avseenden.
Hur skiljs dessa ömsesidigt uteslutande faktorer åt?
Ibland handlar det helt enkelt om det finansiella flödets karaktär - till exempel olja kontra tekniska produkter/tjänster.
Ibland kallas de för faktorer - till exempel momentum, storlek, kvalitet, värde osv.
Dessutom är ömsesidig exklusivitet viktig vid optionshandel, där vinsten för en option ofta kan baseras på att en annan händelse inte inträffar. I detta sammanhang hjälper ömsesidig exklusivitet näringsidkare att skydda sina risker och hantera sin exponering.
Experiment (Bernoulli-försök)
Ett Bernoulli-experiment är ett grundläggande begrepp inom sannolikhetsteorin som avser en slumpmässig händelse med endast två möjliga utfall.
Att kasta ett mynt är till exempel ett Bernoulliförsök, där de möjliga utfallen är krona eller klave.
Ett annat exempel är huruvida en viss optionshandel kommer att ge resultat (in-the-money) eller inte (out-of-the-money) vid utgången.
I sannolikhetsteorin definieras sannolikheten för framgång (dvs. det intressanta resultatet) med p, och sannolikheten för misslyckande (dvs. det alternativa resultatet) med q = 1 - p.
Resultaten av ett Bernoulli-försök betecknas ofta med 1 för framgång och 0 för misslyckande.
Betydelsen av Bernoulliförsök inom handel och investeringar är att vissa finansiella beslut innebär binära utfall.
Du kan till exempel besluta att köpa en aktieoption i hopp om att den kommer att gå jämnt ut, eller så kan du välja att sälja den i hopp om att dess pris kommer att gå jämnt ut och att du får hela premien.
I båda fallen är resultatet binärt i termer av pengar. Ren binär satsning tar formen av binära optioner.
Genom att tillämpa sannolikhetsteorins principer på handel och investeringar kan du fatta mer välgrundade beslut om när du ska köpa eller sälja.
Det finns också begrepp som förväntat värde, som lär dig att inte alltid satsa på det mest sannolika utfallet.
Sannolikhetsfördelning
Inom sannolikhetsteorin är en sannolikhetsfördelning en funktion som beskriver sannolikheten för olika utfall i ett slumpmässigt experiment eller en slumpmässig process.
Den anger sannolikheterna för alla möjliga utfall av en händelse, och summan av sannolikheterna för alla utfall är lika med ett.
Det finns många typer av sannolikhetsfördelningar, men de vanligaste är normalfördelningen, binomialfördelningen och Poissonfördelningen.
Varje fördelning har sin egen uppsättning parametrar som bestämmer dess form, och dessa parametrar används ofta för att göra förutsägelser och fatta beslut.
På finansmarknaderna tenderar naturligtvis avkastningen att ha bredare svansar och passar inte in i en förutbestämd fördelning, så den tenderar att anpassas.
Sammantaget är sannolikhetsfördelningar viktiga eftersom de ger en ram för att förstå den risk och osäkerhet som är förknippad med finansiella investeringar.
Ett av de viktigaste begreppen inom handel/investeringar är att allting är en sannolikhet (dvs. en fördelning av möjliga utfall). Det finns inget enskilt särskilt sannolikt utfall.
Genom att använda sannolikhetsfördelningar kan handlare och investerare uppskatta sannolikheten för olika utfall och fatta mer välgrundade beslut om hur de ska fördela sina resurser.
En näringsidkare kan t.ex. använda normalfördelningen eller en grovstjärtad fördelning för att modellera den dagliga avkastningen på en viss aktie.
Han kan sedan använda denna fördelning för att uppskatta sannolikheten för att aktiens avkastning kommer att överstiga ett visst tröskelvärde, till exempel en avkastning på +/-5 % på en dag.
Genom att använda sannolikhetsfördelningar på detta sätt kan handlare bättre hantera sina risker och optimera sin avkastning.
Förutom att uppskatta sannolikheter används sannolikhetsfördelningar också för att skapa finansiella instrument som optioner och terminer.
Dessa instrument prissätts baserat på den underliggande fördelningen av den tillgång som de är kopplade till, och näringsidkare kan använda dem för att skydda sin risk eller göra satsningar på framtida prisrörelser för tillgången.
Dessutom kan fördelningar konstrueras utifrån priset på de underliggande optionerna, vilket visas nedan.
Fördelning som diskonterats av marknaderna :
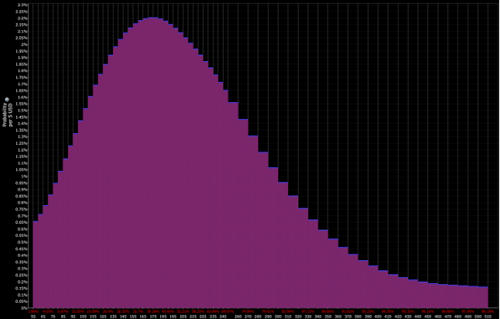
Distributionen bestäms av näringsidkaren (vilket öppnar dörren för taktiska möjligheter):
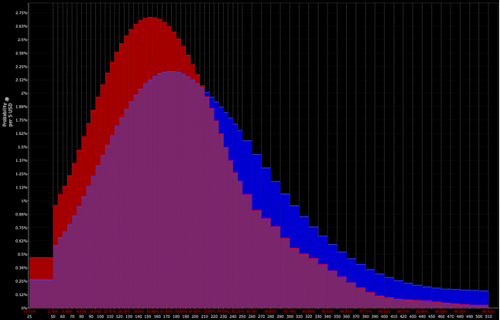
Binomialfördelning
Binomialfördelningen är en sannolikhetsfördelning som modellerar antalet positiva resultat i en serie oberoende och identiska försök, där varje försök endast har två möjliga resultat (t.ex. krona eller klave, vinna eller förlora, högt eller lågt).
De viktigaste parametrarna i binomialfördelningen är sannolikheten för framgång vid ett enda försök (betecknas p) och antalet försök (betecknas n).
Binomialfördelningen är viktig inom handel och investeringar eftersom den kan användas för att modellera fördelningen av avkastningen från en binär handelsstrategi (t.ex. en strategi som innebär att man köper eller säljer en tillgång beroende på om en viss händelse inträffar).
I synnerhet kan det förväntade värdet av en binär handelsstrategi beräknas med hjälp av binomialfördelningen.
Det förväntade värdet av en binär handelsstrategi är summan av produkterna av sannolikheten för varje möjligt utfall och avkastningen på detta utfall.
Om en binär handelsstrategi till exempel har en sannolikhet på 60 % att uppnå en avkastning på 10 % och en sannolikhet på 40 % att uppnå en avkastning på -5 %, är strategins förväntade värde följande
(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04
Binomialfördelningen kan användas för att beräkna sannolikheten för varje möjligt resultat i en serie binära affärer.
Om en näringsidkare till exempel gör 10 binära affärer med 60 % sannolikhet för framgång och 40 % sannolikhet för misslyckande, kan sannolikheten för att göra ett visst antal lyckade affärer (dvs. en viss framgångsfrekvens) beräknas med hjälp av binomialfördelningen.
Detta kan hjälpa näringsidkaren att bedöma risken och den potentiella avkastningen för sin handelsstrategi.
Förväntat värde
Vi har diskuterat förväntat värde (FV) i andra artiklar, eftersom det är ett grundläggande begrepp inom sannolikhetsteorin som beskriver det genomsnittliga resultatet av en slumpmässig variabel.
Inom handel och investeringar används förväntat värde för att beräkna den potentiella avkastningen och risken för en investerings- eller handelsstrategi.
Matematiskt sett är det förväntade värdet av en slumpvariabel summan av produkterna av varje möjligt utfall och dess sannolikhet.
Tänk till exempel på ett myntkast som ger 1 dollar för krona och 0 dollar för klave.
Det förväntade värdet av detta myntkast är följande:
FV = (0,5 * 1 DOLLAR) + (0,5 * 0 DOLLAR) = 0,50 DOLLAR
Detta innebär att den genomsnittliga vinsten för detta myntkast är 0,50 dollar. Detta kommer att ge dig en break-even-punkt över tid, eftersom dina odds matchar den faktiska sannolikheten.
Inom handel och investeringar används förväntat värde för att uppskatta den potentiella avkastningen av en handelsstrategi eller investering.
Om en aktie till exempel har 60 % chans att öka i värde med 10 % och 40 % chans att minska i värde med 5 %, kan den förväntade avkastningen på investeringen beräknas på följande sätt:
FV = (0,6 * 10 %) + (0,4 * -5 %) = 6 % - 2 % = 4 %.
Detta innebär att den förväntade avkastningen på investeringen är 4 %.
Denna information kan hjälpa investerare och handlare att besluta om att investera i aktien och att bedöma risken och den potentiella avkastningen av deras investering.
Det förväntade värdet är också viktigt inom riskhantering.
Genom att beräkna det förväntade värdet av en handelsstrategi eller investering kan handlare och investerare bedöma den potentiella risken med investeringen.
Om till exempel det förväntade värdet för en investering är negativt betyder det att investeringen sannolikt kommer att förlora pengar i genomsnitt på lång sikt.
Handlare/investerare kan använda denna information för att hantera sin risk genom att diversifiera sina investeringar eller begränsa sin exponering för investeringen eller transaktionen.
Dessutom, som vi också har diskuterat i andra artiklar, är det inte alltid det bästa beslutet att satsa på det resultat som har det högsta förväntade värdet.
Ibland är det bättre att ha ett lägre förväntat värde om det ger en lägre varians (lägre risk för förlust eller misslyckande). Dessutom vill du alltid se till att du kan täcka förlusten.
Om du till exempel har 1 000 dollar och du har 90 % chans att fördubbla dina pengar till 2 000 dollar och 10 % chans att förlora hela 1 000 dollar är ditt EV mycket högt (1 800 dollar - 1 000 dollar = +800 dollar).
Men om du inte har råd att förlora 1 000 dollar om du gör ett misstag är det bättre att inte fatta beslutet.
Markovkedja
Markovkedja är ett matematiskt begrepp från sannolikhetsteorin som beskriver en process där nästa steg eller tillstånd endast beror på det aktuella tillståndet och inte på tidigare tillstånd.
Med andra ord är det en minneslös process som endast bygger på det aktuella tillståndet för att bestämma det framtida tillståndet.
En Markovkedja definieras av en uppsättning tillstånd och sannolikheterna för att gå från ett tillstånd till ett annat.
Dessa sannolikheter representeras ofta i en övergångsmatris, där varje element i matrisen representerar sannolikheten att gå från ett tillstånd till ett annat.
Markovkedjan är viktig inom handel och investeringar eftersom den kan användas för att modellera finansmarknadernas beteende.
Aktiemarknaden är till exempel ett komplext system med ett stort antal variabler som påverkar priset på de värdepapper som ingår i den.
Markovkedjan gör det möjligt att förenkla systemet genom att endast fokusera på marknadens nuvarande tillstånd och sannolikheten för att den ska övergå till andra tillstånd.
Genom att modellera aktiemarknaden som en Markov-kedja kan handlare och investerare potentiellt få ytterligare insikt genom att förutsäga framtida marknadsrörelser baserat på det aktuella marknadstillståndet.
Markovkedjan kan också användas för att hjälpa till att beräkna olika mått som förväntad avkastning, volatilitet och risk.
Dessutom används Markovkedjan i olika finansiella modelleringstekniker som optionsprissättning, portföljoptimering och riskhantering.
Den gör det möjligt för handlare/investerare att skapa och testa olika investeringsstrategier och att mäta effektiviteten hos dessa strategier under olika marknadsförhållanden.
Slumpmässig vandring
Random walk är ett matematiskt begrepp från sannolikhetsteorin som beskriver ett föremåls rörelse på ett slumpmässigt och oförutsägbart sätt.
I en random walk bestäms objektets nästa position av en slumpmässig process, t.ex. genom att kasta ett mynt eller en tärning.
Inom finansbranschen används ofta en random walk-modell för att beskriva aktiekursernas utveckling över tiden.
Teorin bakom denna modell är att aktiekursernas rörelser är oförutsägbara och följer ett slumpmässigt mönster.
Detta innebär att det är lika troligt att priset på en aktie vid en viss tidpunkt kommer att stiga som att det kommer att sjunka, och att aktiekursens rörelse över tiden inte påverkas av tidigare priser eller andra externa faktorer. (Naturligtvis finns det olika idéer och teorier om trender, momentum osv.)
Begreppet random walk är användbart att känna till inom handel och investeringar eftersom det tyder på att det är mycket svårt att förutsäga aktiekursernas utveckling.
Detta innebär att det är svårt att konsekvent slå marknaden genom att köpa och sälja aktier baserat på tidigare prisrörelser eller annan information.
Investerare och handlare kan använda begreppet random walk för att stödja sin investeringsstrategi och fatta mer välgrundade beslut.
De kan till exempel välja att investera i en diversifierad portfölj av aktier för att minska sin exponering för enskilda aktiers prisrörelser och diversifiera efter tillgångar, tillgångsklasser, länder och valutor, och överväga att använda en köp- och behållningsstrategi för att undvika de kostnader och risker som är förknippade med frekvent handel.
Stokastisk process
Den stokastiska processen är en matematisk ram som används för att modellera beteendet hos ett system som utvecklas slumpmässigt över tiden.
Det är en samling slumpmässiga variabler som är indexerade med tiden, vilket innebär att processens värde vid varje given tidpunkt är slumpmässigt.
Stokastiska processer är användbara inom sannolikhetsteorin eftersom de kan hjälpa oss att analysera beteendet hos slumpmässiga fenomen som utvecklas över tiden.
De ger ett sätt att modellera och förstå slumpmässigheten i dessa fenomen, vilket kan användas för att göra förutsägelser och fatta beslut som bygger på förväntade resultat.
Inom handel och investeringar används stokastiska processer för att modellera vissa beteenden hos finansmarknader och tillgångspriser.
De gör det möjligt att analysera slumpmässighet och volatilitet i finansiella data, vilket kan användas för att fatta beslut om när tillgångar ska köpas eller säljas.
Stokastiska processer kan till exempel användas för att modellera aktiekursers eller växelkursers rörelser, vilket kan hjälpa handlare och investerare att göra förutsägelser om framtida rörelser på dessa marknader.
Stokastiska processer används också för att utveckla och testa handelsstrategier. Genom att simulera finansmarknadernas beteende med hjälp av stokastiska processer kan handlare och investerare testa sina handelsstrategier och utvärdera deras prestanda under olika marknadsförhållanden.
Villkorlig sannolikhet
Villkorlig sannolikhet är ett grundläggande begrepp inom sannolikhetsteorin som avser sannolikheten för att en händelse inträffar om en annan händelse redan har inträffat. Det är ett sätt att uppdatera våra sannolikhetsbedömningar på grundval av ny information.
Mer formellt definieras den betingade sannolikheten för en händelse A om händelse B har inträffat på följande sätt:
P(A | B) = P(A och B) / P(B)
Där :
- P(A och B) är sannolikheten för att både händelserna A och B inträffar, och
- P(B) är sannolikheten för att händelse B inträffar.
Villkorlig sannolikhet är viktigt inom handel och investeringar eftersom det gör det möjligt för oss att uppdatera våra sannolikhetsbedömningar när ny information blir tillgänglig.
Om vi till exempel vet att ett företag just har tillkännagivit en positiv resultatrapport är den betingade sannolikheten för att aktiekursen kommer att stiga på grund av denna information högre än före tillkännagivandet.
Investerare och handlare använder villkorlig sannolikhet för att fatta bättre informerade beslut på grundval av ny information.
Genom att uppdatera sina sannolikhetsbedömningar kan de bättre bedöma de potentiella riskerna och vinsterna med en viss investering.
Detta kan hjälpa dem att göra mer lönsamma affärer och hantera sina risker mer effektivt.
Anta till exempel att en investerare överväger att köpa en aktie som alltid har varit volatil.
Med hjälp av villkorlig sannolikhet kan investeraren bedöma sannolikheten för att aktiekursen kommer att stiga eller sjunka utifrån olika marknadsförhållanden, t.ex. förändringar i räntor, tillväxt, inflation, politik eller geopolitiska händelser.
Denna information kan hjälpa investeraren att fatta ett mer välgrundat beslut om huruvida aktien ska köpas, behållas eller säljas.
Lagen om stora tal
Lagen om stora tal är ett grundläggande begrepp inom sannolikhetsteorin som beskriver hur medelvärdet av ett stort antal oberoende slumpvariabler beter sig.
Denna lag säger att när antalet oberoende försök ökar, konvergerar genomsnittet av dessa försök mot det förväntade värdet för den underliggande sannolikhetsfördelningen.
Förenklat uttryckt innebär lagen om stora tal att ju fler gånger ett experiment upprepas, desto närmare kommer de observerade resultaten att ligga det förväntade resultatet.
Exempel på ett myntkast
Om du till exempel kastar ett mynt upprepade gånger, förutsäger lagen om stora tal att frekvensen av huvuden kommer att närma sig 50 % när antalet kast ökar.
Av 1 000 kast är det ytterst osannolikt att ett rättvist mynt får 55/45 i båda riktningarna (0,17 %), men det är fullt möjligt av 100 kast (36,8 %).
Varför det är användbart
Lagen om stora tal är användbar inom handel och investeringar eftersom den hjälper till att minska risken för oförutsägbara marknadsfluktuationer.
Genom att investera i en diversifierad portfölj kan en investerare sprida sin risk över ett stort antal tillgångar, vilket kan bidra till att minska effekten av prisrörelser i enskilda tillgångar.
Dessutom är lagen om stora tal användbar för att analysera historiska marknadsdata för att fatta välgrundade investeringsbeslut.
Genom att undersöka ett stort antal historiska marknadstrender kan investerare hjälpa till att identifiera mönster och trender som kan hjälpa dem att fatta mer välgrundade investeringsbeslut.
Om en näringsidkare till exempel vill veta om Federal Reserve någonsin har sänkt räntorna trots en inflation över målet kan han eller hon titta på historien för att se om det finns prejudikat och vilken effekt det har haft på olika tillgångsmarknader.
Om det finns ett urval, hur stort är det för att få tillräckligt med användbara uppgifter för att kunna dra användbara slutsatser?
Hur förhåller sig lagen om stora tal till statistisk signifikans?
Lagen om stora tal och statistisk signifikans är relaterade begrepp inom statistiken, men de är inte identiska.
Lagen om stora tal hänvisar till det faktum att urvalets medelvärde av ett stort antal oberoende observationer konvergerar mot det förväntade värdet av den underliggande sannolikhetsfördelningen när antalet observationer närmar sig oändligheten.
Statistisk signifikans är å andra sidan ett mått på sannolikheten för att de observerade resultaten av en undersökning inte beror på slumpen.
Vid statistisk hypotesprövning anses ett resultat vara statistiskt signifikant om sannolikheten för att det observerade resultatet ska vara slumpmässigt är lägre än ett fördefinierat tröskelvärde, vanligen 5 % eller mindre.
I praktiken kan lagen om stora tal användas för att stödja statistisk signifikans.
När ett stort urval samlas in och urvalets medelvärde ligger nära det förväntade värdet för den underliggande fördelningen, tyder detta på att det är mindre sannolikt att de observerade resultaten beror på slumpen och mer sannolikt att de är statistiskt signifikanta.
Det är dock viktigt att notera att statistisk signifikans inte nödvändigtvis innebär praktisk betydelse eller ekonomisk relevans, och att statistisk signifikans i sig inte bör användas för att fatta viktiga beslut.
För att kunna fatta välgrundade beslut är det viktigt att ha en god förståelse för de underliggande uppgifterna, de statistiska metoderna och sammanhanget för det problem som studeras.
Bayes' teorem
Bayes teorem är ett grundläggande begrepp inom sannolikhetsteorin som beskriver hur man uppdaterar sannolikheterna baserat på nya bevis eller ny information.
Det är uppkallat efter pastor Thomas Bayes, en brittisk statistiker och teolog från 1700-talet.
Teoremet ger ett sätt att beräkna sannolikheten för en hypotes eller händelse utifrån tidigare kunskaper eller uppfattningar (kallad prioritets sannolikhet) och nya bevis (kallad sannolikhet).
Den uppdaterade sannolikheten kallas den efterföljande sannolikheten och representerar sannolikheten för hypotesen eller händelsen efter att hänsyn tagits till de nya bevisen.
Formeln för Bayes sats är följande:
P(A|B) = P(B|A) * P(A) / P(B)
Där :
- P(A|B) är den efterföljande sannolikheten för händelse A med tanke på bevis B.
- P(B|A) är sannolikheten för bevis B givet händelse A
- P(A) är den tidigare sannolikheten för händelse A, och
- P(B) är sannolikheten för bevis B.
Bayes' teorem är användbart inom handel och investeringar eftersom det kan hjälpa investerare att uppdatera sina uppfattningar om sannolikheten för olika händelser utifrån ny information, t.ex. nyheter om ett företags resultat eller ekonomiska indikatorer.
Och detta är en viktig aspekt av Bayes sannolikhet: den uppdaterar dina tidigare trosuppfattningar utan att nödvändigtvis bestämma eller räkna om dem från början.
Genom att använda Bayes teorem kan investerare uppdatera sina sannolikheter och fatta mer välgrundade investeringsbeslut.
Exempel på vikten av att testa våra antaganden
Bankkassörska
Ett berömt exempel på Bayes teorem i praktiken kommer från Kahnemans och Tverskys studie.
I denna studie fick deltagarna följande information:
Linda är 31 år gammal, singel, frispråkig och mycket intelligent. Hon har studerat filosofi. Som student var hon mycket engagerad i frågor om diskriminering och social rättvisa och deltog även i protester mot kärnkraft.
Deltagarna ombads sedan att rangordna sannolikheten för två möjliga scenarier:
- Linda är bankkassörska.
- Linda är bankkassörska och är aktiv i den feministiska rörelsen.
Trots att det första scenariot omfattar fler personer (alla bankkassörer) än det andra (bankkassör och feminist), rankade många deltagare det andra scenariot som mer sannolikt.
Detta beror på att Lindas beskrivning stämmer överens med deras stereotyp av en feminist, även om sannolikheten för att båda händelserna ska inträffa är lägre än sannolikheten för den första händelsen.
Detta exempel visar hur viktigt det är att testa våra antaganden och ta hänsyn till all tillgänglig information innan vi fattar beslut.
Bayes teorem kan hjälpa investerare att uppdatera sina sannolikheter och undvika bias som kan leda till felaktiga beslut.
Är Steve en bonde eller en bibliotekarie?
Den berömda studien utförd av Kahneman och Tversky involverade ett annat scenario där deltagarna var tvungna att bestämma sannolikheten för att Steve var antingen en bonde eller en bibliotekarie, baserat på begränsad information om hans personlighet.
Deltagarna fick följande information:
Steve är en tystlåten, blyg person som gillar att läsa böcker och inte är särskilt social.
Enbart baserat på denna information drog de flesta deltagare slutsatsen att Steve var mer sannolikt att vara bibliotekarie än bonde. Kahneman och Tversky visade dock att denna slutsats inte nödvändigtvis var motiverad.
För att visa detta gav de deltagarna ytterligare information som var relevant men som inte fanns med i den initiala beskrivningen.
Till exempel lade de till information om antalet bönder kontra bibliotekarier och andelen bönder med Steves personlighetstyp, vilket fortfarande gav ett högre antal bönder än det totala antalet bibliotekarier.
Till exempel, om det finns 20 gånger fler bönder än bibliotekarier och 20 % av bönderna passar denna personlighetstyp, är det fortfarande 4 gånger (20 * 0,20) mer sannolikt att Steve är bonde än bibliotekarie.
När deltagarna fick denna nya information ökade deras odds att Steve var en bonde avsevärt, vilket tyder på att deras initiala slutsatser inte var tillräckligt informerade.
Denna studie belyser vikten av att testa antaganden när man fattar beslut baserat på begränsad information.
Det är viktigt att överväga alla relevanta faktorer och inte bara förlita sig på initiala antaganden eller heuristik, såsom stereotyper, när man fattar beslut eller gör bedömningar.
Detta tillvägagångssätt överensstämmer med det Bayesianska synsättet på sannolikhet, vilket innebär att kontinuerligt uppdatera föreställningar baserat på ny information.
När det gäller handel och investeringar är det alltid viktigt att fråga hur vet du att du vet?
Korrelation och kovarians
Korrelation och kovarians är två statistiska begrepp som ofta används inom sannolikhetsteorin för att beskriva förhållandet mellan två slumpmässiga variabler.
Kovarians mäter i vilken utsträckning två slumpvariabler rör sig tillsammans, medan korrelation mäter styrkan och riktningen på deras förhållande.
En positiv kovarians visar att de två variablerna tenderar att röra sig i samma riktning, medan en negativ kovarians visar att de tenderar att röra sig i motsatt riktning.
En korrelationskoefficient varierar mellan -1 och 1, där värden på 1 indikerar en perfekt positiv korrelation, värden på -1 indikerar en perfekt negativ korrelation och värden på 0 indikerar ingen korrelation.
Inom handel/investeringar är korrelation och kovarians användbara verktyg för riskhantering och portföljspridning.
Genom att förstå förhållandet mellan olika tillgångar kan investerare bättre förvalta sina portföljer genom att välja tillgångar som inte är starkt korrelerade med varandra.
Detta kan bidra till att minska den totala portföljrisken genom att sprida investeringarna över olika tillgångsklasser och sektorer.
Till exempel kan en portfölj med starkt korrelerade aktier vara mer riskfylld än en portfölj med lågt korrelerade aktier eller andra tillgångar.
Genom att välja ett diversifierat utbud av tillgångar med låg korrelation kan en investerare skapa en mer motståndskraftig portfölj som är mindre benägen att drabbas av betydande förluster på en nedåtgående marknad.
Att förstå korrelation och kovarians kan dessutom hjälpa investerare att identifiera mönster på marknaden och förutsäga framtida trender.
Det är också viktigt att förstå att korrelationer är bakåtblickande och tenderar att förändras med tiden.
Till exempel kan aktier och obligationer vara negativt korrelerade i en miljö där förändringarna i den diskonterade inflationen minskar, men kan vara positivt korrelerade i miljöer där den diskonterade inflationen ökar.
Mer robusta tolkningar av inflationen kommer således att titta närmare på tillgångarnas inneboende tillstånd på grundval av kausala ekonomiska samband, snarare än bakåtblickande tolkningar som enkla korrelationskoefficienter, som bara är flyktiga biprodukter av den miljö där de befinner sig.
CFD-mäklare
Vanliga frågor - Sannolikhetsteori inom handel
Vad är sannolikhetsteori och varför är den viktig inom handel?
Sannolikhetsteori är en gren av matematiken som behandlar analysen av slumpmässiga fenomen.
Den ger en ram för att förstå sannolikheten för händelser och beteendet hos system som uppvisar slumpmässighet.
Sannolikhetsteorin är ett viktigt verktyg för att fatta välgrundade beslut i situationer där utgången är osäker.
Inom handelsområdet är sannolikhetsteorin avgörande för att förstå riskerna och den potentiella avkastningen av olika investeringsstrategier.
Handlare använder sannolikhetsteorin för att bedöma sannolikheten för att vissa händelser ska inträffa, t.ex. sannolikheten för att en aktie ska öka i värde eller att en viktig händelse ska inträffa.
De använder den också för att beräkna det förväntade värdet av sina affärer, dvs. den genomsnittliga vinst eller förlust som de kan förvänta sig att göra på lång sikt.
Genom att använda sannolikhetsteori kan handlare fatta mer välgrundade beslut om när de ska gå in i eller lämna en handel, hur mycket de ska investera och hur de ska hantera risken.
De kan också använda den för att utveckla och testa handelsstrategier för att se hur de fungerar under olika marknadsförhållanden.
Vilka är de viktigaste sannolikhetsbegreppen för näringsidkare att förstå?
Det finns flera viktiga sannolikhetsbegrepp som näringsidkare måste förstå.
Här är några av dem:
- Sannolikhetsfördelningar: Sannolikhetsfördelningar beskriver sannolikheten för olika utfall i en slumpmässig händelse. Handlare använder sannolikhetsfördelningar för att förstå det potentiella intervallet av utfall för en viss handel. Vanligt förekommande sannolikhetsfördelningar inom handel är normalfördelningen, som beskriver beteendet hos många finansiella variabler, och binomialfördelningen, som används för att modellera binära utfall.
- Förväntat värde: Det förväntade värdet av en handel är den genomsnittliga vinst eller förlust som kan förväntas på lång sikt. Genom att beräkna det förväntade värdet kan näringsidkare bedöma den potentiella lönsamheten i en handel och fatta mer välgrundade beslut om att gå in i eller lämna handeln.
- Standardavvikelse: Standardavvikelse: Standardavvikelse är ett mått på mängden variation eller volatilitet i en datamängd. Handlare använder standardavvikelse för att förstå risknivån förknippad med en viss handel. Högre nivåer av standardavvikelse indikerar högre risknivåer. Observera att standardavvikelsen är baserad på normalfördelningen, som inte passar in på många finansiella tillgångar/variabler.
- Korrelation: Korrelationen mäter styrkan och riktningen på förhållandet mellan två variabler. Vid handel använder handlare korrelation för att förstå hur olika tillgångar rör sig i förhållande till varandra. En hög positiv korrelation mellan två tillgångar tyder på att de tenderar att röra sig i samma riktning, medan en negativ korrelation tyder på att de tenderar att röra sig i motsatt riktning.
- Statistisk signifikans: Statistisk signifikans avser sannolikheten för att ett observerat resultat inte beror på slumpen. Handlare använder statistisk signifikans för att bedöma effektiviteten hos en handelsstrategi eller för att avgöra om en viss händelse sannolikt kommer att ha en betydande inverkan på marknaden.
Att förstå dessa och andra sannolikhetsbegrepp kan hjälpa näringsidkare att fatta bättre beslut på marknaderna och hantera sina risker mer effektivt.
Slutsats - Sannolikhetsteori inom handel
Sannolikhetsteorin spelar en viktig roll inom handel, eftersom den hjälper handlare att fatta välgrundade beslut baserade på datadriven analys.
Med hjälp av sannolikhetsteorin kan handlare uppskatta sannolikheten för potentiella marknadsrörelser och utveckla handelsstrategier för att dra nytta av dessa rörelser.
Den hjälper näringsidkare att bedöma risk och belöning för en handel, förvalta sin portfölj och optimera sina positioner.
Sannolikhetsteorin är särskilt användbar när det gäller att kvantifiera osäkerhet och mäta marknadens volatilitet, vilket gör det möjligt för näringsidkare att förutse och förbereda sig för marknadsförändringar.
På det hela taget ger sannolikhetsteorin näringsidkare verktygen för att fatta mer välinformerade och exakta handelsbeslut, vilket kan leda till större lönsamhet och minskad risk.
| Föregående : Kovarians - tillämpningar inom handel och portföljkonstruktion | Följande : Hur man skapar ett handelssystem |
