Teoria da probabilidades e trading

O que é a teoria da probabilidade e porque é importante?

A teoria da probabilidade é essencial na negociação e no investimento porque permite aos participantes no mercado compreender e quantificar a incerteza e o risco associado às decisões financeiras.

Tal como a própria vida, a negociação é sobre probabilidades. Raramente há resultados óbvios, a preto e branco, que são fáceis de capitalizar.

Utilizando a teoria das probabilidades, os traders/investidores podem tomar decisões mais informadas com base na probabilidade de vários resultados.

Aqui estão algumas razões pelas quais a teoria da probabilidade é tão importante no trading/investimento:

Quantificar o risco

A teoria da probabilidades permite aos investidores calcular a probabilidade de várias coisas acontecerem, incluindo cenários positivos e negativos.

Isto permite aos traders compreender melhor os riscos potenciais associados a diferentes negócios/investimentos.

Tomada de decisões

A teoria da probabilidade permite aos traders tomar melhores decisões com base na probabilidade de resultados diferentes e através da avaliação das próprias probabilidades (o que pode ser chamado de "probabilidade de probabilidades", uma vez que as probabilidades de diferentes coisas acontecerem não são conhecidas por si próprias).

Por exemplo, se um investimento ou transacção tem uma probabilidade de 70% de produzir um retorno positivo durante um ano, como se sabe?

A teoria da probabilidade abrange coisas como a variância e como gerir melhor o que não se sabe e não se pode saber.

Gestão de Portfólio

A teoria da probabilidade ajuda os traders/investidores a gerir as suas carteiras, fornecendo uma forma de avaliar o risco associado às diferentes classes de activos.

Ao analisar a probabilidade de diferentes resultados, os traders/investidores podem criar uma carteira diversificada que equilibra o risco e o retorno.

Gestão do risco

A teoria da probabilidade também é importante na gestão do risco, uma vez que ajuda os investidores a determinar a probabilidade de eventos que possam ter um impacto negativo nos seus investimentos/operações e a tomar medidas para os mitigar.

Em geral, a teoria da probabilidade é uma ferramenta importante para os investidores/traders compreenderem os riscos e recompensas potenciais das diferentes oportunidades de investimento, fazerem escolhas mais informadas e alcançarem melhores resultados a longo prazo.

Neste artigo, iremos analisar os diferentes ramos da teoria da probabilidade e as suas aplicações no trading.

Aleatoriedade

Na teoria da probabilidade, a aleatoriedade refere-se ao facto de que o resultado de um evento é imprevisível e pode variar de julgamento para julgamento.

Este fenómeno é frequentemente modelado utilizando distribuições de probabilidade, que descrevem a probabilidade de cada resultado possível.

A aleatoriedade é um conceito fundamental na teoria da probabilidade porque nos permite quantificar o que é desconhecido e fazer previsões sobre o futuro com base em informação incompleta.

Em muitas situações do mundo real, os resultados dos acontecimentos são afectados por um grande número de variáveis difíceis ou impossíveis de prever com certeza/precisão.

A aleatoriedade permite-nos ter isto em conta e estimar a probabilidade de vários resultados com base em dados históricos, causalidade económica ou outra informação.

No trading e no investimento, a aleatoriedade está sempre presente porque os mercados financeiros estão sujeitos a uma vasta gama de influências.

Existem muitos tipos diferentes de pessoas nos mercados, de tamanhos diferentes, e com motivações diferentes para negociar.

A aleatoriedade pode manifestar-se sob a forma de volatilidade do mercado, eventos inesperados ou outros factores que podem causar movimentos de preços rápidos e imprevisíveis.

Compreender e ter em conta esta aleatoriedade é essencial para desenvolver estratégias de trading bem sucedidas e gerir o risco.

Quanto mais experiência as pessoas ganham nos mercados, mais se apercebem de que tudo o que sabem é palpável em comparação com as coisas que precisam de saber com base no que é actualizado nos mercados.

Uma forma de comerciantes e investidores poderem lidar com a aleatoriedade é utilizar modelos baseados na probabilidade para tomar decisões.

Por exemplo, um trader pode utilizar um modelo estatístico para estimar a probabilidade de um aumento ou queda no preço de um determinado activo durante um determinado período. Esta informação pode então ser utilizada para construir uma carteira bem equilibrada e gerir o risco.

Por exemplo, se a distribuição de preços com desconto para um determinado activo for semelhante à seguinte

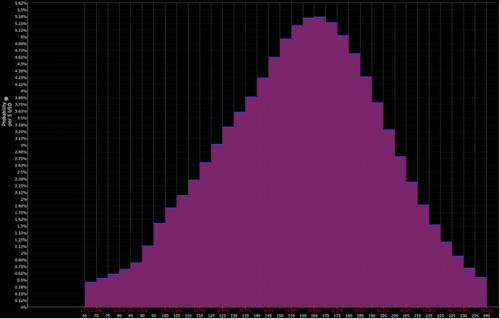
E a interpretação do operador está mais próxima da combinação da distribuição vermelha e roxa (ou seja, uma inclinação em baixa):

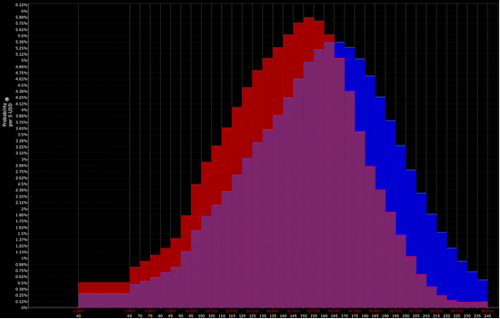
Podem então esperar tomar uma posição de baixa sobre o bem. Depois, é claro, há a questão de como o montar e o tamanho.

Exclusividade Mútua

Na teoria da probabilidade, o conceito de exclusividade mútua refere-se à propriedade de dois eventos que são diferentes um do outro.

Matematicamente, diz-se que dois eventos A e B são mutuamente exclusivos se a sua intersecção (ou seja, o evento em que tanto A como B ocorrem) estiver vazia, ou seja, P(A ∩ B) = 0.

A exclusividade mútua é importante no trading/investimento porque ajuda os investidores a compreender melhor como gerir os seus riscos.

Quando os investidores possuem uma carteira de activos, precisam de considerar as correlações entre/entre os seus activos.

Por exemplo, digamos que um trader/investidor tem uma carteira de acções que inclui tanto empresas tecnológicas como petrolíferas. Se o preço do petróleo subir, isto pode ajudar as empresas petrolíferas, mas os stocks de tecnologia podem sofrer (por exemplo, devido ao efeito negativo do aumento dos preços do petróleo sobre as taxas de juro), e vice-versa.

No entanto, se houver desenvolvimentos em cada sector, estes podem não influenciar os preços das reservas no outro sector.

Assim, embora os títulos estejam relacionados entre si em alguns aspectos - tais como alterações no crescimento com desconto e inflação - em outros aspectos excluem-se mutuamente.

Como são separados estes factores mutuamente exclusivos?

Por vezes é simplesmente a natureza do fluxo financeiro - por exemplo, petróleo versus produtos/serviços tecnológicos.

Por vezes, são chamados factores - por exemplo, dinâmica, tamanho, qualidade, valor, etc.

Além disso, a exclusividade mútua é importante no trading de opções, onde o pagamento de uma opção pode muitas vezes ser baseado na não ocorrência de outro evento. Neste contexto, a exclusividade mútua ajuda os operadores a cobrir os seus riscos e a gerir a sua exposição.

Experiência (julgamento Bernoulli)

Uma experiência ou julgamento Bernoulli é um conceito fundamental na teoria da probabilidade que se refere a um evento aleatório com apenas dois resultados possíveis.

Por exemplo, o lançamento de uma moeda é um ensaio de Bernoulli, onde os resultados possíveis são cabeças ou caudas.

Outro exemplo é se uma determinada opção de comércio compensará (in-the-money) ou não (out-of-the-money) no vencimento.

Na teoria da probabilidade, a probabilidade de sucesso (ou seja, o resultado do interesse) é definida por p, e a probabilidade de fracasso (ou seja, o resultado alternativo) por q = 1 - p.

Os resultados de um julgamento Bernoulli são frequentemente assinalados por 1 para o sucesso e 0 para o fracasso.

A importância dos ensaios Bernoulli no comércio e no investimento é que algumas decisões financeiras envolvem resultados binários.

Por exemplo, pode decidir comprar uma opção de compra de acções na esperança de que esta se equilibre, ou pode optar por vendê-la na esperança de que o seu preço se equilibre e que receba o prémio total.

Em qualquer dos casos, o resultado é binário em termos de dinheiro. As apostas binárias puras assumem a forma de opções binárias.

Ao aplicar os princípios da teoria da probabilidade ao trading e ao investimento, pode tomar decisões mais informadas sobre quando comprar ou vender.

Há também conceitos como o valor esperado, que lhe ensinam a não apostar sempre no resultado mais provável.

Distribuição de probabilidades

Na teoria da probabilidade, uma distribuição de probabilidade é uma função que descreve a probabilidade de diferentes resultados numa experiência ou processo aleatório.

Ela especifica as probabilidades de todos os resultados possíveis de um evento, e a soma das probabilidades de todos os resultados é igual a um.

Existem muitos tipos de distribuição de probabilidades, mas as mais comuns incluem a distribuição normal, a distribuição binomial e a distribuição de Poisson.

Cada distribuição tem o seu próprio conjunto de parâmetros que determinam a sua forma, e estes parâmetros são frequentemente utilizados para fazer previsões e tomar decisões.

Evidentemente, nos mercados financeiros, os retornos tendem a ter caudas mais largas e não cabem numa distribuição pré-determinada, pelo que tendem a ser personalizados.

Globalmente, as distribuições de probabilidade são importantes porque fornecem um quadro para a compreensão do risco e incerteza associados aos investimentos financeiros.

Um dos conceitos mais importantes no trading/investimento é que tudo é uma probabilidade (ou seja, uma distribuição de resultados potenciais). Não existe um único resultado particularmente provável.

Ao utilizar distribuições de probabilidade, traders e investidores podem estimar a probabilidade de diferentes resultados e tomar decisões mais informadas sobre como alocar os seus recursos.

Por exemplo, um trader pode utilizar a distribuição normal ou uma distribuição grosseira para modelar os retornos diários sobre um determinado stock.

Pode então utilizar esta distribuição para estimar a probabilidade de o retorno do stock exceder um determinado limiar, por exemplo um retorno de +/-5% num dia.

Ao utilizar as distribuições de probabilidade desta forma, os traders podem gerir melhor o seu risco e optimizar os seus retornos.

Além de estimar probabilidades, as distribuições de probabilidade são também utilizadas para criar instrumentos financeiros, tais como opções e futuros.

Estes instrumentos são fixados com base na distribuição subjacente do activo ao qual estão ligados, e os traders podem utilizá-los para cobrir o seu risco ou fazer apostas em movimentos futuros do preço do activo.

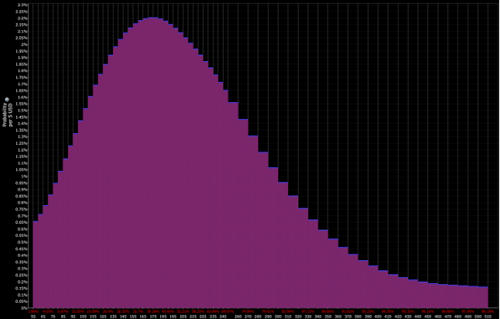
Além disso, as distribuições podem ser construídas com base no preço das opções subjacentes, como se mostra abaixo.

Distribuição com desconto por parte dos mercados :

Distribuição determinada pelo trader (que abre a porta a oportunidades tácticas):

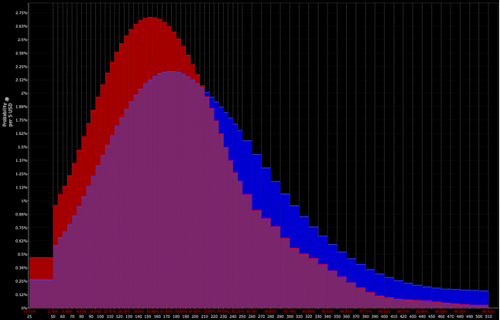
Distribuição binomial

A distribuição binomial é uma distribuição de probabilidade que modela o número de resultados positivos numa série de ensaios independentes e idênticos, em que cada ensaio tem apenas dois resultados possíveis (por exemplo, cabeça ou cauda, ganhar ou perder, alto ou baixo).

Os parâmetros chave da distribuição binomial são a probabilidade de sucesso num único ensaio (denotada por p) e o número de ensaios (denotado por n).

A distribuição binomial é importante no campo do trading e do investimento porque pode ser usada para modelar a distribuição dos retornos de uma estratégia de trading binomial (por exemplo, uma estratégia que envolve a compra ou venda de um activo, dependendo da ocorrência de um determinado evento).

Em particular, o valor esperado de uma estratégia de trading binomial pode ser calculado utilizando a distribuição binomial.

O valor esperado de uma estratégia de trading binomial é a soma dos produtos da probabilidade de cada resultado possível e o retorno desse resultado.

Por exemplo, se uma estratégia de trading binomial tiver uma probabilidade de 60% de alcançar um retorno de 10% e uma probabilidade de 40% de alcançar um retorno de -5%, o valor esperado da estratégia é

(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04

A distribuição binomial pode ser utilizada para calcular as probabilidades de cada resultado possível numa série de transacções binomiais.

Por exemplo, se um trader fizer 10 transacções binárias com uma probabilidade de 60% de sucesso e uma probabilidade de fracasso de 40%, a probabilidade de fazer um certo número de transacções com sucesso (ou seja, uma certa taxa de sucesso) pode ser calculada utilizando a distribuição binomial.

Isto pode ajudar o trader a avaliar o risco e o potencial retorno da sua estratégia de trading.

Valor esperado

Discutimos o valor esperado (VE) noutros artigos, pois é um conceito fundamental na teoria da probabilidade que descreve o resultado médio de uma variável aleatória.

No campo do trading e do investimento, o valor esperado é utilizado para calcular o potencial retorno e risco de um investimento ou estratégia de trading.

Matematicamente, o valor esperado de uma variável aleatória é a soma dos produtos de cada resultado possível e a sua probabilidade.

Por exemplo, considere um lançamento de moeda que rende $1 para as cabeças e $0 para os rabos.

O valor esperado deste atiramento de moeda é o seguinte:

VE = (0,5 * $1) + (0,5 * $0) = $0,50

Isto significa que o pagamento médio para este arremesso de moeda é de $0,50. Isto dar-lhe-á um ponto de equilíbrio ao longo do tempo, uma vez que as suas probabilidades coincidem com a probabilidade real.

No trading e no investimento, o valor esperado é utilizado para estimar os retornos potenciais de uma estratégia de trading ou investimento.

Por exemplo, se uma acção tem uma probabilidade de 60% de aumentar o seu valor em 10% e uma probabilidade de 40% de diminuir o seu valor em 5%, o retorno esperado do investimento pode ser calculado da seguinte forma:

VE = (0,6 * 10%) + (0,4 * -5%) = 6% - 2% = 4%

Isto significa que o retorno esperado do investimento é de 4%.

Esta informação pode ajudar investidores e comerciantes a decidir investir no stock, e a avaliar o risco e o potencial retorno do seu investimento.

O valor esperado é também importante na gestão do risco.

Ao calcular o valor esperado de uma estratégia de trading ou investimento, os traders e os investidores podem avaliar o risco potencial do investimento.

Por exemplo, se o valor esperado de um investimento for negativo, significa que o investimento é susceptível de perder dinheiro, em média, a longo prazo.

Os traders/investidores podem utilizar esta informação para gerir o seu risco, diversificando os seus investimentos ou limitando a sua exposição ao investimento ou transacção.

Além disso, como também discutimos noutros artigos, apostar no resultado com o maior valor esperado nem sempre é a melhor decisão.

Por vezes, é melhor ter um valor esperado mais baixo se isso lhe der uma variação menor (menor risco de perda ou falha). Além disso, quer ter sempre a certeza de que pode cobrir a perda.

Por exemplo, se tiver $1.000 e tiver 90% de probabilidade de duplicar o seu dinheiro para $2.000 e 10% de probabilidade de perder os $1.000, o seu VE é muito elevado ($1.800 - $1.000 = +$800).

Mas se não puder perder os $1.000 no caso de cometer um erro, é melhor não tomar a decisão.

Corrente Markov

A cadeia de Markov é um conceito matemático da teoria da probabilidade que descreve um processo em que o próximo passo ou estado depende apenas do estado actual e não dos estados anteriores.

Por outras palavras, é um processo sem memória que depende apenas do seu estado actual para determinar o seu estado futuro.

Uma cadeia de Markov é definida por um conjunto de estados e as probabilidades de passar de um estado para outro.

Estas probabilidades são frequentemente representadas numa matriz de transição, onde cada elemento da matriz representa a probabilidade de se deslocar de um estado para outro.

A cadeia de Markov é importante no domínio do trading/investimento porque pode ser utilizada para modelar o comportamento dos mercados financeiros.

A bolsa de valores, por exemplo, é um sistema complexo com um grande número de variáveis que afectam o preço dos seus títulos constituintes.

A cadeia Markov permite que o sistema seja simplificado, concentrando-se apenas no estado actual do mercado e nas probabilidades de se deslocar para outros estados.

Ao modelar a bolsa de valores como uma cadeia de Markov, traders e investidores podem potencialmente ganhar conhecimentos adicionais ao preverem movimentos futuros do mercado com base no estado actual do mercado.

A cadeia de Markov também pode ser utilizada para ajudar a calcular várias medidas, tais como retornos esperados, volatilidade e risco.

Além disso, a cadeia de Markov é utilizada em várias técnicas de modelização financeira, tais como o preço de opções, a optimização de carteiras e a gestão de risco.

Permite aos traders/investidores criar e testar diferentes estratégias de investimento, e medir a eficácia destas estratégias em diferentes condições de mercado.

Passeio aleatório

O passeio aleatório é um conceito matemático da teoria da probabilidade que descreve o movimento de um objecto de uma forma aleatória e imprevisível.

Numa caminhada aleatória, a posição seguinte do objecto é determinada por um processo aleatório, tal como o atirar de uma moeda ou de um dado.

Nas finanças, um modelo de passeio aleatório é frequentemente utilizado para descrever a evolução dos preços das acções ao longo do tempo.

A teoria por detrás deste modelo é que o movimento dos preços das acções é imprevisível e segue um padrão aleatório.

Isto significa que o preço de uma acção num determinado momento é tão susceptível de subir como de descer, e que o movimento do preço da acção ao longo do tempo não é influenciado por preços passados ou outros factores externos. (Claro que existem várias ideias e teorias sobre tendências, dinâmica, etc.).

O conceito de um passeio aleatório é útil para conhecer no trading e no investimento porque sugere que é muito difícil prever a evolução dos preços das acções.

Isto significa que é difícil vencer consistentemente o mercado através da compra e venda de acções com base em movimentos de preços passados ou outras informações.

Investidores e traders podem utilizar o conceito de passeio aleatório para apoiar a sua estratégia de investimento e tomar decisões mais informadas.

Por exemplo, podem optar por investir numa carteira diversificada de acções para reduzir a sua exposição aos movimentos individuais dos preços das acções e diversificar por activos, classes de activos, países e moedas, e considerar a utilização de uma estratégia de compra e venda para evitar os custos e riscos da negociação frequente.

Processo estocástico

O processo estocástico é uma estrutura matemática utilizada para modelar o comportamento de um sistema que evolui de forma aleatória ao longo do tempo.

É uma colecção de variáveis aleatórias indexadas pelo tempo, o que significa que o valor do processo num dado momento é aleatório.

Os processos estocásticos são úteis na teoria da probabilidade porque podem ajudar-nos a analisar o comportamento de fenómenos aleatórios que evoluem ao longo do tempo.

Fornecem uma forma de modelização e compreensão da aleatoriedade destes fenómenos, que pode ser utilizada para fazer previsões e tomar decisões com base nos resultados esperados.

No domínio do trading e do investimento, são utilizados processos estocásticos para modelar certos comportamentos dos mercados financeiros e dos preços dos activos.

Eles permitem a análise da aleatoriedade e volatilidade dos dados financeiros, que podem ser utilizados para tomar decisões sobre quando comprar ou vender activos.

Por exemplo, os processos estocásticos podem ser utilizados para modelar o movimento dos preços das acções ou das taxas de câmbio, o que pode ajudar traders e investidores a fazer previsões sobre os movimentos futuros nestes mercados.

Os processos estocásticos são também utilizados para desenvolver e testar estratégias de trading. Através da simulação do comportamento dos mercados financeiros utilizando processos estocásticos, traders e investidores podem testar as suas estratégias de trading e avaliar o seu desempenho sob diferentes condições de mercado.

Probabilidade condicional

A probabilidade condicional é um conceito fundamental na teoria da probabilidade que se refere à probabilidade da ocorrência de um evento se já tiver ocorrido outro evento. É uma forma de actualizar as nossas estimativas de probabilidade com base em novas informações.

Mais formalmente, a probabilidade condicional de um evento A, dado que o evento B já ocorreu, é definida como se segue:

P(A | B) = P(A e B) / P(B)

Onde :

• P(A e B) é a probabilidade de que ambos os eventos A e B ocorram, e
• P(B) é a probabilidade de ocorrência do evento B.

A probabilidade condicional é importante no trading e no investimento porque nos permite actualizar as nossas estimativas de probabilidade à medida que novas informações se tornam disponíveis.

Por exemplo, se soubermos que uma empresa acaba de anunciar um relatório de ganhos positivos, a probabilidade condicional de o preço da acção subir com base nesta informação é maior do que antes do anúncio.

Investidores e traders utilizam a probabilidade condicional para tomar decisões mais bem informadas com base em novas informações.

Ao actualizar as suas estimativas de probabilidade, podem avaliar melhor os riscos e recompensas potenciais de um dado investimento.

Isto pode ajudá-los a fazer negócios mais rentáveis e a gerir os seus riscos de forma mais eficaz.

Por exemplo, suponha que um investidor está a considerar comprar uma acção que sempre foi volátil.

Utilizando a probabilidade condicional, o investidor pode avaliar a probabilidade de o preço das acções subir ou descer com base em várias condições de mercado, tais como alterações nas taxas de juro, crescimento, inflação, política ou eventos geopolíticos.

Esta informação pode ajudar o investidor a tomar uma decisão mais informada sobre se deve comprar, deter ou vender a acção.

Lei dos grandes números

A lei dos grandes números é um conceito fundamental na teoria da probabilidade que descreve o comportamento da média de um grande número de variáveis aleatórias independentes.

Esta lei afirma que à medida que o número de julgamentos independentes aumenta, a média desses julgamentos converge para o valor esperado da distribuição de probabilidade subjacente.

Em termos mais simples, a lei de grandes números afirma que quanto mais vezes uma experiência for repetida, mais próximos estarão os resultados observados do resultado esperado.

Exemplo de atirar uma moeda ao ar

Por exemplo, se se atirar uma moeda ao ar repetidamente, a lei dos grandes números prevê que a frequência das cabeças se aproximará dos 50% à medida que o número de voltas aumentar.

De 1.000 fichas, é extremamente improvável que uma moeda justa suba 55/45 em qualquer dos sentidos (0,17%), mas é bastante possível em 100 fichas (36,8%).

Porque é útil

A lei dos grandes números é útil no trading e no investimento porque ajuda a mitigar o risco de flutuações imprevisíveis do mercado.

Ao investir numa carteira diversificada, um investidor pode repartir o seu risco por um grande número de activos, o que pode ajudar a reduzir o impacto dos movimentos de preços em activos individuais.

Além disso, a lei dos grandes números é útil para analisar dados históricos do mercado para tomar decisões de investimento informadas.

Ao examinar um grande número de tendências históricas do mercado, os investidores podem ajudar a identificar padrões e tendências que os possam ajudar a tomar decisões de investimento mais informadas.

Por exemplo, se um comerciante quiser saber se a Reserva Federal alguma vez reduziu as taxas de juro apesar da inflação acima do objectivo, pode olhar para a história para ver se existem precedentes e o efeito que teve em vários mercados de activos.

Se houver uma amostra, qual é a dimensão para obter dados úteis suficientes para determinar conclusões úteis?

Como é que a lei dos grandes números se relaciona com o significado estatístico?

A lei dos grandes números e a significância estatística são conceitos relacionados em estatísticas, mas não são idênticos.

A lei dos grandes números refere-se ao facto de a média amostral de um grande número de observações independentes convergir para o valor esperado da distribuição de probabilidade subjacente, à medida que o número de observações se aproxima do infinito.

O significado estatístico, por outro lado, é uma medida da probabilidade de os resultados observados de um estudo não serem devidos ao acaso.

No teste de hipóteses estatísticas, um resultado é considerado estatisticamente significativo se a probabilidade de obter o resultado observado por acaso for inferior a um limiar pré-definido, normalmente 5% ou menos.

Na prática, a lei dos grandes números pode ser utilizada para apoiar a significância estatística.

Quando uma grande amostra é recolhida e a média da amostra está próxima do valor esperado da distribuição subjacente, isto sugere que os resultados observados têm menos probabilidades de serem devidos ao acaso e mais probabilidades de serem estatisticamente significativos.

Contudo, é importante notar que a significância estatística não implica necessariamente significado prático ou relevância económica, e que a significância estatística por si só não deve ser utilizada para tomar decisões importantes.

Para tomar decisões informadas, é essencial ter uma boa compreensão dos dados subjacentes, dos métodos estatísticos e do contexto do problema em estudo.

Teorema de Bayes

O teorema de Bayes é um conceito fundamental na teoria da probabilidade que descreve como actualizar as probabilidades com base em novas provas ou informações.

O seu nome vem do Reverendo Thomas Bayes, um estatístico e teólogo britânico do século XVIII.

O teorema fornece uma forma de calcular a probabilidade de uma hipótese ou evento com base em conhecimento ou crenças anteriores (chamada probabilidade anterior) e nova evidência (chamada verosimilhança).

A probabilidade actualizada é chamada probabilidade posterior, e representa a probabilidade da hipótese ou evento depois de se ter em conta a nova evidência.

A fórmula para o teorema de Bayes é a seguinte:

P(A|B) = P(B|A) * P(A) / P(B)

Onde :

• P(A|B) é a probabilidade posterior do evento A dado o evento B
• P(B|A) é a probabilidade de prova B dado evento A
• P(A) é a probabilidade prévia do evento A, e
• P(B) é a probabilidade de prova B

O teorema de Bayes é útil no trading e no investimento porque pode ajudar os investidores a actualizar as suas crenças sobre a probabilidade de diferentes eventos com base em novas informações, tais como notícias sobre os ganhos de uma empresa ou indicadores económicos.

E este é um aspecto chave da probabilidade Bayesiana: actualiza as suas crenças anteriores, sem necessariamente as determinar ou recalcular a partir do zero.

Ao utilizar o teorema de Bayes, os investidores podem actualizar as suas probabilidades e tomar decisões de investimento mais informadas.

Exemplos da importância de testar os nossos pressupostos

Caixa de banco

Um famoso exemplo do teorema de Bayes em acção vem do estudo de Kahneman e Tversky.

Neste estudo, os participantes receberam as seguintes informações:

Linda tem 31 anos de idade, é solteira, franca e muito inteligente. Ela estudou filosofia. Como estudante, estava muito preocupada com questões de discriminação e justiça social, tendo também participado em protestos anti-nucleares.

Os participantes foram então convidados a classificar a probabilidade de dois cenários possíveis:

• Linda é uma caixa de banco.
• Linda é uma caixa de banco e é activa no movimento feminista.

Apesar do facto de o primeiro cenário incluir mais pessoas (todas as caixas bancárias) do que o segundo (caixa bancária e feminista), muitos participantes classificaram o segundo cenário como mais provável.

Isto porque a descrição de Linda encaixa no seu estereótipo de feminista, embora a probabilidade de ambos os eventos ocorrerem seja menor do que a probabilidade do primeiro evento.

Este exemplo demonstra a importância de testar os nossos pressupostos e de ter em conta toda a informação disponível antes de tomar decisões.

O teorema de Bayes pode ajudar os investidores a actualizar as suas probabilidades e evitar enviesamentos que podem levar a decisões incorrectas.

Steve é um agricultor ou um bibliotecário?

O famoso estudo de Kahneman e Tversky envolveu outro cenário em que foi pedido aos participantes que determinassem a probabilidade de Steve ser um agricultor ou um bibliotecário, com base em informações limitadas sobre a sua personalidade.

Os participantes receberam as seguintes informações:

Steve é um indivíduo calado e tímido que gosta de ler livros e não é muito social.

Com base apenas nesta informação, a maioria dos participantes concluiu que Steve era mais provável que fosse um bibliotecário do que um agricultor. No entanto, Kahneman e Tversky mostraram que esta conclusão não era necessariamente justificada.

Para demonstrar isto, apresentaram aos participantes informações adicionais que eram relevantes mas não incluídas na descrição inicial.

Por exemplo, adicionaram informações sobre o número de agricultores versus bibliotecários e a percentagem de agricultores com o tipo de personalidade de Steve, o que ainda resultou num número de agricultores superior ao número total de bibliotecários.

Por exemplo, se houver 20x tantos agricultores como bibliotecários e 20% dos agricultores com este tipo de personalidade, ainda é 4x (20 * 0,20) mais provável que Steve seja um agricultor do que um bibliotecário.

Quando os participantes receberam esta nova informação, as suas probabilidades de Steve ser um agricultor aumentaram significativamente, indicando que as suas conclusões iniciais não foram suficientemente informadas.

Este estudo salienta a importância de testar os pressupostos quando se tomam decisões baseadas em informação limitada.

É importante considerar todos os factores relevantes e não confiar apenas em pressupostos ou heurísticas iniciais, tais como estereótipos, quando se tomam decisões ou julgamentos.

Esta abordagem é consistente com a abordagem Bayesiana da probabilidade, que envolve a actualização contínua das crenças em resposta a novas informações.

No trading e no investimento, é sempre importante perguntar como é que se sabe que se sabe?

Correlação e covariância

Correlação e covariância são dois conceitos estatísticos comummente utilizados na teoria da probabilidade para descrever a relação entre duas variáveis aleatórias.

A covariância mede a medida em que duas variáveis aleatórias se movem em conjunto, enquanto a correlação mede a força e a direcção da sua relação.

Uma covariância positiva indica que as duas variáveis tendem a mover-se na mesma direcção, enquanto uma covariância negativa indica que elas tendem a mover-se em direcções opostas.

Um coeficiente de correlação varia de -1 a 1, com valores de 1 indicando uma correlação positiva perfeita, valores de -1 indicando uma correlação negativa perfeita, e valores de 0 indicando sem correlação.

No trading/investimento, a correlação e a covariância são ferramentas úteis para a gestão do risco e a diversificação da carteira.

Ao compreenderem a relação entre diferentes activos, os investidores podem gerir melhor as suas carteiras seleccionando activos que não estejam altamente correlacionados uns com os outros.

Isto pode ajudar a reduzir o risco global das carteiras, espalhando os investimentos por diferentes classes de activos e sectores.

Por exemplo, uma carteira de acções altamente correlacionadas pode ser mais arriscada do que uma carteira de acções pouco correlacionadas ou outros activos.

Ao seleccionar uma gama diversificada de activos com baixa correlação, um investidor pode criar uma carteira mais resiliente e menos susceptível de sofrer perdas significativas num mercado em baixa.

Além disso, a compreensão da correlação e da covariância pode ajudar os investidores a identificar padrões no mercado e a prever tendências futuras.

É também importante compreender que as correlações são retrógradas e tendem a mudar ao longo do tempo.

Por exemplo, as acções e obrigações podem estar negativamente correlacionadas num ambiente em que as mudanças na inflação descontada estão a diminuir, mas podem estar positivamente correlacionadas em ambientes em que a inflação descontada está a aumentar.

Assim, as interpretações mais robustas da inflação olharão mais de perto para o estado intrínseco dos activos com base em ligações económicas causais, em vez de interpretações retrógradas, tais como simples coeficientes de correlação, que são apenas subprodutos fugazes do ambiente em que se encontram.

Brokers de CFD

CFD Brokers	Plataformas	Regulamentado pela	Abrir uma conta de demonstração
	MetaTrader 4 e 5 AvaOptions	ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM
	xStation 5	FCA, KNF, CySEC, BIFSC, CNMV, DFSA
	MetaTrader 4 y 5 cTrader TradingView	FCA, ASIC, CySEC, BaFin, DFSA, SCB, CMA
	MetaTrader 4 et 5 Markets Webtrader	FCA, BaFin, ASIC, FINMA, FSCA, MAS, FMA, DFSA, JFSA, CFTC
	MetaTrader 4 e 5	FCA, ASIC, CySEC, JSC, OCRCVM, FSCA
ASIC: Austrália, BaFin: Alemanha, BIFSC: Belize, BVI FSC: Ilhas Virgens Britânicas, BACEN e CVM: Brasil, CySEC: Chipre, CNMV: Espanha, CMVM: Portugal, CSSF: Luxemburgo, CFTC: EUA, CBFSAI: Irlanda, CMA : Omã, DFSA: Dubai, FCA: Reino Unido, FINMA: Suíça, FSPR - FMA: Nova Zelândia, FRSA: Abu Dhabi, FSA: Seychelles, FSCA: África do Sul, JFSA: Japão, JSC: Jordânia, KNF: Polônia, MAS: Singapura, IIROC: Canadá, SCB: Bahamas, VFSC: Vanuatu
A negociação de CFD envolve um risco significativo de perda, pelo que não é adequado para todos os investidores. 74-89% das contas de pequenos investidores perdem dinheiro a negociar CFDs.

FAQs - Teoria da Probabilidade no Trading

Conclusão - Teoria da Probabilidade no Trading

A teoria da probabilidade desempenha um papel crucial no trading, uma vez que ajuda os comerciantes a tomarem decisões informadas com base em análises orientadas por dados.

Usando a teoria da probabilidade, os traders podem estimar a probabilidade de potenciais movimentos de mercado e desenvolver estratégias de trading para capitalizar esses movimentos.

Ajuda os traders a avaliar o risco-recompensa de uma negociação, gerir a sua carteira e optimizar as suas posições.

A teoria da probabilidade é particularmente útil para quantificar a incerteza e medir a volatilidade do mercado, permitindo aos traders antecipar e preparar-se para as mudanças do mercado.

Em geral, a teoria da probabilidade fornece aos traders as ferramentas para tomar decisões de trading mais informadas e precisas, o que pode levar a uma maior rentabilidade e a uma redução do risco.