 |  |  |  |  |  |
Broker de CFD
Red Social
Criptomonedas
Cuentas financiadas
Cálculo de la varianza en el trading y la inversión
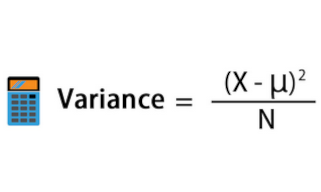
La varianza desempeña un papel importante en el trading y la inversión porque mide el grado de dispersión de los rendimientos en torno al rendimiento medio.
En otras palabras, la varianza indica en qué medida los rendimientos de un valor o una cartera se desvían de su rendimiento medio.
Los inversores y traders utilizan la varianza (volatilidad) para estimar el riesgo de una inversión.
Una varianza más alta significa que hay más incertidumbre y riesgo asociados a la inversión, mientras que una varianza más baja indica menos riesgo.
Puntos clave a recordar - Varianza
- La varianza mide el grado de dispersión de los rendimientos en torno al rendimiento medio de un valor o una cartera.
- Una varianza elevada indica mayor incertidumbre y riesgo asociados a la inversión, mientras que una varianza baja indica menor riesgo.
- Los traders y los inversores utilizan la varianza para determinar el tamaño óptimo de la posición de una operación y para diversificar sus carteras con el fin de gestionar el riesgo.
Fórmula de la varianza
La fórmula de la varianza es una expresión matemática que calcula la dispersión o variabilidad de un conjunto de puntos de datos.
Se define como la media de las diferencias al cuadrado entre cada punto de datos y la media del conjunto.
La fórmula de la varianza es la siguiente:
Varianza = Σ (xi - μ)² / n
donde:
- Σ es el símbolo de suma (que significa "suma de").
- xi es el valor del i-ésimo punto de datos del conjunto
- μ es el valor medio del conjunto.
- n es el número total de puntos de datos del conjunto.
Para calcular la varianza, primero hay que calcular la media del conjunto de datos.
A continuación, para cada punto de datos, se resta la media del punto de datos, se eleva al cuadrado la diferencia y se añade a la suma.
Por último, se divide la suma por el número total de puntos de datos para obtener la varianza.
La fórmula de la varianza se utiliza en muchos cálculos estadísticos, como las pruebas de hipótesis, el análisis de regresión y el control de calidad.
También es un elemento clave en el cálculo de otras medidas estadísticas, como la desviación típica, que es la raíz cuadrada de la varianza.
¿Cómo se utiliza la varianza en el trading?
En el trading, la varianza se utiliza a menudo para determinar el tamaño de posición óptimo para una operación.
Al conocer la varianza esperada de una acción o cartera, los operadores pueden determinar la cantidad de riesgo que están dispuestos a asumir y ajustar el tamaño de su posición en consecuencia.
Por ejemplo, si la varianza es elevada, un operador puede decidir reducir el tamaño de su posición para limitar las pérdidas potenciales.
En la gestión de carteras, la varianza desempeña un papel clave en la diversificación.
Una cartera bien diversificada incluirá activos con diferentes niveles naturales de varianza, reduciendo así el riesgo global de la cartera.
Combinando estos tipos de activos, los inversores pueden crear una cartera que alcance el nivel de riesgo deseado al tiempo que maximiza la rentabilidad.
En general, la varianza es una medida esencial para inversores y traders, ya que les ayuda a comprender el nivel de riesgo asociado a una inversión y a tomar decisiones informadas sobre la gestión de la cartera y las estrategias de trading.
Varianza y desviación típica
Tanto la varianza como la desviación típica miden la variabilidad o dispersión de un conjunto de datos.
Sin embargo, la desviación típica se utiliza más en el trading y las inversiones, ya que sirve para medir la volatilidad.
Varianza
La varianza es una medida estadística de la diferencia entre los puntos de datos de un conjunto y la media de ese conjunto.
Se calcula hallando la media de las diferencias al cuadrado entre cada punto de datos y la media del conjunto.
Una mayor varianza indica que los puntos de datos están más dispersos y alejados de la media.
Desviación típica
La desviación típica es la raíz cuadrada de la varianza.
Es una medida de lo alejados que están los puntos de datos de la media del conjunto. La desviación típica se utiliza a menudo en el trading y la inversión para medir la volatilidad de una acción o cartera.
Una desviación típica más alta indica que los rendimientos de la acción o cartera son más volátiles o arriesgados.
En el trading y la inversión, es importante comprender la variabilidad de los rendimientos porque puede indicar el nivel de riesgo asociado a una inversión concreta.
Por ejemplo, un inversor puede preferir una acción con una desviación típica baja porque es menos volátil y ofrece una rentabilidad más estable a lo largo del tiempo.
Sin embargo, una desviación típica más alta puede ser preferida por un inversor más tolerante al riesgo, dispuesto a aceptar una mayor volatilidad a cambio de una rentabilidad potencialmente más alta.
Es entonces cuando los traders/inversores empiezan a hablar de cosas como "rentabilidad ajustada al riesgo" o ratios como Sharpe, Sortino, Treynor y otras formas de medición de la rentabilidad ajustada al riesgo.
En general, la desviación típica es una medida más útil en el trading y la inversión, ya que proporciona una comprensión más intuitiva de la variabilidad de los rendimientos, y se utiliza ampliamente en modelos y análisis financieros.
Tipos de varianza en estadística
En estadística, la varianza es una medida de la dispersión de un conjunto de datos. Existen varios tipos de varianza que se utilizan habitualmente en el análisis estadístico.
Algunos de los tipos de varianza más comunes son
Varianza poblacional
La varianza poblacional es la varianza de toda una población.
Mide la dispersión de los datos en la población.
Varianza de la muestra
La varianza muestral es la varianza de una muestra de datos.
Se utiliza para estimar la varianza de la población.
Como la muestra suele ser más pequeña que la población, la varianza de la muestra será diferente de la varianza de la población.
Varianza intragrupo
La varianza intragrupo es la varianza dentro de un grupo de datos.
Se utiliza en el análisis de la varianza (ANOVA) para determinar si existen diferencias significativas entre los grupos.
Varianza entre grupos
La varianza entre grupos es la varianza entre grupos de datos.
También se utiliza en ANOVA para determinar si existen diferencias significativas entre los grupos.
Varianza residual
La varianza residual es la varianza que queda después de ajustar un modelo a los datos. Mide hasta qué punto el modelo es capaz de explicar la variabilidad de los datos.
Cada uno de estos tipos de varianza tiene un uso específico en el análisis estadístico. Es importante elegir el tipo de varianza adecuado para el análisis que se está realizando para garantizar unos resultados precisos y significativos.
Varianza y covarianza
La varianza y la covarianza son dos conceptos importantes en el trading y las finanzas, ya que cuantifican la volatilidad y la correlación de los activos de una cartera.
La varianza mide la variabilidad de los rendimientos de un único activo, mientras que la covarianza mide la variabilidad conjunta de los rendimientos de dos activos.
En el trading, la varianza se utiliza a menudo para medir la volatilidad, o el grado en que los rendimientos de un activo varían con el tiempo.
La volatilidad es un factor importante para los traders, ya que afecta al riesgo y a la recompensa potencial de una inversión.
Una varianza más alta indica un mayor grado de volatilidad y riesgo, mientras que una varianza más baja indica menos volatilidad y riesgo.
La covarianza, por su parte, mide el movimiento conjunto de dos activos. Una covarianza positiva indica que los dos activos tienden a moverse en la misma dirección, mientras que una covarianza negativa indica que tienden a moverse en direcciones opuestas.
La covarianza es importante para los traders porque les ayuda a diversificar su cartera identificando activos que no estén muy correlacionados entre sí. Esto puede ayudar a reducir el riesgo global y aumentar la rentabilidad potencial.
En resumen, la varianza mide la volatilidad de un único activo, mientras que la covarianza mide la correlación entre dos activos. Ambos conceptos son importantes en el trading y las finanzas, y pueden utilizarse para gestionar el riesgo y aumentar la rentabilidad potencial de una cartera.
Compensación media-varianza
La compensación media-varianza es un concepto fundamental de las finanzas que se refiere a la compensación entre el rendimiento esperado y el riesgo (o varianza) de una inversión.
En otras palabras, los inversores pueden elegir entre asumir más riesgo a cambio de una rentabilidad potencialmente mayor o aceptar una rentabilidad menor a cambio de un riesgo menor.
En el contexto del trading y la inversión, la relación media-varianza se utiliza a menudo para construir carteras que optimicen el equilibrio entre riesgo y rentabilidad.
La teoría moderna de carteras, desarrollada por Harry Markowitz, proporciona un marco para determinar la cartera óptima que logra la mayor rentabilidad esperada para un nivel de riesgo dado.
La teoría parte del supuesto de que los inversores tienen aversión al riesgo y prefieren carteras que minimicen el riesgo para un nivel determinado de rentabilidad o maximicen la rentabilidad para un nivel determinado de riesgo.
En la práctica, los inversores utilizan herramientas como el Modelo de Valoración de Activos de Capital (CAPM) y la frontera eficiente para determinar la asignación óptima de carteras.
El CAPM utiliza la rentabilidad esperada del mercado, el tipo sin riesgo y la beta del valor para calcular la rentabilidad esperada de un activo, mientras que la frontera eficiente identifica el conjunto de carteras que ofrecen la mayor rentabilidad esperada para un determinado nivel de riesgo.
Los inversores deben tener en cuenta la relación media-varianza para tomar decisiones de inversión bien fundadas.
Las inversiones de alto riesgo y alta rentabilidad pueden ser adecuadas para algunos inversores, mientras que otros pueden preferir inversiones de bajo riesgo y baja rentabilidad.
Una cartera bien diversificada que incluya una combinación de activos con distintos niveles de riesgo puede ayudar a lograr un equilibrio más óptimo entre riesgo y rentabilidad.
Varianza y valor esperado
En el trading y la inversión, la varianza y el valor esperado son dos conceptos importantes que ayudan a los inversores a tomar decisiones informadas sobre sus inversiones.
El valor esperado (VE) es una medida del resultado medio de una determinada inversión o estrategia de trading.
Es la suma de los resultados ponderados por probabilidad de todos los escenarios posibles.
Por ejemplo, si un inversor tiene un 60% de probabilidades de obtener un 10% de rentabilidad de una inversión y un 40% de perder un 5%, el valor esperado de la inversión es
- (0,6 * 0,10) + (0,4 * -0,05) = 0,06 - 0,02 = 0,04, es decir, una rentabilidad esperada del 4%.
La varianza mide la dispersión o desviación de los posibles resultados en torno al valor esperado.
Una varianza elevada indica que es probable que el resultado real se desvíe significativamente del valor esperado, mientras que una varianza baja indica que es probable que el resultado real se aproxime al valor esperado.
En otras palabras, la varianza es una medida del riesgo asociado a una inversión o estrategia de trading.
Por ejemplo, si dos inversiones tienen el mismo rendimiento esperado del 10%, pero una tiene una varianza alta y la otra una varianza baja, la inversión de varianza alta es más arriesgada porque es probable que sus rendimientos reales sean más dispersos e impredecibles.
Los inversores y los traders utilizan tanto el valor esperado como la varianza para evaluar y comparar las oportunidades de inversión.
Pueden preferir inversiones con un valor esperado alto y una varianza baja, lo que indica que la inversión tiene potencial para generar grandes rendimientos al tiempo que es relativamente predecible.
Sin embargo, algunos inversores pueden estar dispuestos a asumir un mayor riesgo y aceptar una mayor varianza para lograr mayores rendimientos.
Ejemplo lúdico de varianza respecto al valor esperado
Supongamos que juegas a un juego con tres opciones:
- Opción 1: 80% de posibilidades de ganar 10.000 $.
- Opción 2: 30% de posibilidades de ganar 100.000 $.
- Opción 3: 10% de posibilidades de ganar 1.000.000 $.
Tus valores esperados en cada situación son
- 8,000 $
- 30,000 $
- 100,000 $
¿Sacrificaría el VE por una varianza menor?
El tipo de persona que elegiría cada opción en función de su tolerancia al riesgo y su situación financiera variaría en función de sus preferencias individuales, sus objetivos financieros y su actitud ante el riesgo.
Opción 1
Una persona con aversión al riesgo y baja capacidad de riesgo financiero puede elegir la Opción 1 porque ofrece una mayor probabilidad de ganar, aunque la recompensa sea menor.
Esta persona puede valorar la seguridad de un pago más garantizado y estar dispuesta a sacrificar la posibilidad de ganar una mayor cantidad de dinero para evitar el riesgo de perderlo todo.
Opción 2
Una persona con una tolerancia al riesgo moderada y una mayor capacidad para asumir riesgos financieros puede elegir la Opción 2 porque ofrece una recompensa potencial mayor a cambio de asumir un riesgo mayor.
Esta persona puede estar dispuesta a aceptar una menor probabilidad de ganancia a cambio de la posibilidad de ganar una mayor cantidad de dinero.
Sin embargo, es posible que esta persona quiera limitar su exposición al riesgo y no esté dispuesta a arriesgarlo todo por la posibilidad de ganar una gran suma de dinero.
Opción 3
Una persona con una alta tolerancia al riesgo y una gran capacidad de riesgo financiero puede elegir la Opción 3 porque ofrece la mayor recompensa potencial, aunque la probabilidad de ganar sea la más baja.
Esta persona puede estar dispuesta a asumir un mayor nivel de riesgo a cambio de la posibilidad de ganar una suma de dinero mucho mayor.
Sin embargo, esta persona debe estar dispuesta a aceptar el riesgo de perderlo todo por la posibilidad de ganar una suma mucho mayor.
Hay que tener en cuenta que éstas son sólo generalizaciones y que la tolerancia al riesgo y la situación financiera de las personas pueden variar considerablemente en función de sus circunstancias personales, sus objetivos financieros y su psicología.
¿Cómo diseñaría este juego para obtener un tercio de una muestra estadísticamente significativa para cada opción?
Esto requeriría ensayo y error.
Necesitaría un número suficiente de participantes para garantizar la significación estadística y una muestra realmente aleatoria.
Por ejemplo, si elige a jóvenes licenciados universitarios, puede apostar a que votarán mayoritariamente por la primera opción, porque una probabilidad del 80% de tener 10.000 dólares es más valiosa para ellos que apostar por una suma mayor que quizá no tengan.
Por otro lado, si la muestra está formada por empresarios de éxito, la primera opción podría estar infrarrepresentada, porque puede que 10.000 dólares no sean tan importantes para ellos.
Si tuviera una muestra aleatoria con un número de votos estadísticamente significativo y descubriera que domina la opción 1, podría cambiar el juego de la siguiente manera:
- Opción 1: 80% de posibilidades de ganar 10.000 $.
- Opción 2: 50% de posibilidades de ganar 100.000 $.
- Opción 3: 20% de posibilidades de ganar 1.000.000 $.
Sus valores esperados en cada situación serían entonces
- 8,000 $
- 50,000 $
- 200,000 $
Este proceso de ensayo y error es análogo a la forma en que funcionan los mercados en el mundo real.
El "precio de compensación" sería el que recibiera un tercio de los votos en cada uno.
En los mercados financieros, esto podría ser análogo a poseer letras del Tesoro seguras en lugar de acciones o formas de crédito más arriesgadas en lugar de capital riesgo.
Cuanto más se asciende en la escala de riesgo, mayor es el valor esperado, pero a costa de una mayor varianza o riesgo de pérdida o fracaso.
Brokers de CFDs para invertir online
| CFD Brokers | Plataformas | Regulado por la | Abrir una cuenta de demostración |
|---|---|---|---|
| xStation 5 | FCA, KNF, CySEC, BIFSC, CNMV, DFSA |  |
 | MetaTrader 4 y 5 | CySEC, FCA, ASIC, JSC, OCRCVM, FSCA | |
| MetaTrader 4 y 5 | ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM | |
| ASIC: Australia, BaFin: Alemania, BIFSC: Belice, BVI FSC: Islas Vírgenes Británicas, BACEN & CVM: Brasil, CySEC: Chipre, CNMV: España, CMVM: Portugal, CSSF: Luxemburgo, CFTC: EE.UU., CBFSAI: Irlanda, CMA: Omán,, DFSA: Dubai, FCA: Reino Unido, FINMA: Suiza, FSPR - FMA: Nueva Zelanda, FRSA: Abu Dhabi, FSA: Seychelles, FSCA: Sudáfrica, JFSA: Japón, JSC: Jordania, KNF: Polonia, MAS: Singapur, OCRCVM: Canadá, SCB: Bahamas, VFSC: Vanuatu. | |||
| Las operaciones con CFDs implican un importante riesgo de pérdida, por lo que no son adecuadas para todos los inversores. Entre el 74 y el 89% de las cuentas de los inversores minoristas pierden dinero al operar con CFD. | |||
Preguntas frecuentes - Varianza
¿Es lo mismo varianza que volatilidad?
La varianza y la volatilidad son conceptos relacionados, pero no son exactamente lo mismo.
La varianza es una medida estadística que cuantifica la dispersión de un conjunto de puntos de datos en torno a la media.
Se calcula como la media de las diferencias al cuadrado con respecto a la media.
En finanzas, la varianza se utiliza a menudo para medir el riesgo de una cartera o de una acción individual.
La volatilidad, por su parte, es una medida del grado en que el precio de un instrumento financiero varía con el tiempo.
Puede calcularse utilizando diversos métodos, pero un enfoque común es utilizar la desviación típica de los rendimientos del instrumento a lo largo de un periodo determinado.
La volatilidad se utiliza a menudo como indicador de riesgo (o un componente del riesgo), ya que una mayor volatilidad implica un mayor grado de incertidumbre o la posibilidad de que se produzcan grandes oscilaciones de precios.
En finanzas, volatilidad y varianza suelen utilizarse indistintamente, pero no son exactamente lo mismo.
La varianza es un concepto matemático que suele utilizarse como base para calcular la volatilidad, pero la volatilidad es una medida más específica que tiene en cuenta series temporales de precios o rendimientos.
¿Qué es el equilibrio entre sesgo y varianza?
El equilibrio entre sesgo y varianza es un concepto fundamental en el aprendizaje automático que se refiere al equilibrio entre la capacidad de un modelo para ajustarse bien a los datos de entrenamiento (bajo sesgo) y su capacidad para generalizar a nuevos datos no vistos (baja varianza).
El sesgo es la diferencia entre los valores predichos de un modelo y los valores reales de los datos.
Un modelo con un sesgo elevado suele ser excesivamente simplista y no puede captar la complejidad de los datos, lo que da lugar a un ajuste insuficiente.
En otras palabras, el modelo no es capaz de aprender los patrones subyacentes de los datos y sus predicciones son sistemáticamente erróneas.
La varianza es la variabilidad de las predicciones del modelo para diferentes conjuntos de datos de entrenamiento.
Un modelo con una varianza elevada suele ser demasiado complejo y se ha ajustado en exceso a los datos de entrenamiento, lo que da lugar a un modelo que no es capaz de generalizar bien a nuevos datos.
En otras palabras, el modelo ha memorizado los datos de entrenamiento y es incapaz de aplicar lo que ha aprendido a nuevos datos.
El objetivo del aprendizaje automático es encontrar el equilibrio óptimo entre sesgo y varianza, seleccionando un modelo lo bastante complejo como para captar los patrones subyacentes en los datos, pero no tan complejo como para aplicar en exceso los datos de entrenamiento.
Esto puede lograrse seleccionando un modelo de complejidad adecuada, utilizando técnicas de regularización para penalizar los modelos complejos o empleando métodos de conjunto para combinar varios modelos con diferentes sesgos y varianzas.
¿Qué es un swap de varianza?
Un swap de varianza es un contrato financiero que permite a los inversores apostar por el nivel de volatilidad de los precios de un activo subyacente, como una acción, un índice o una materia prima.
El contrato suele estructurarse como un derivado extrabursátil (OTC) e implica un pago basado en la diferencia entre la varianza realizada del precio del activo durante un periodo de tiempo determinado y un nivel de varianza acordado previamente, denominado varianza de ejercicio.
En un swap de varianza, el comprador acuerda pagar una cantidad fija al vendedor a cambio de un pago basado en la diferencia entre la varianza realizada y la varianza de ejercicio.
Si la varianza realizada es mayor que la varianza de ejercicio, el vendedor efectuará un pago al comprador, y viceversa.
Los swaps de varianza suelen ser utilizados por los inversores que desean tener una visión de la volatilidad de un activo, en lugar de su dirección.
Pueden utilizarse con fines de cobertura o especulativos, y suelen emplearlos los creadores de mercado y los inversores institucionales.
Los swaps de varianza pueden personalizarse para satisfacer las necesidades específicas del comprador y el vendedor, como el activo subyacente, la varianza de ejercicio y la duración del contrato.
Conclusión - Varianza
La varianza es una medida estadística que cuantifica la desviación o dispersión de un conjunto de puntos de datos en torno a su media o valor esperado.
En el trading y la inversión, la varianza es un concepto importante que ayuda a los participantes en el mercado a comprender el riesgo asociado a sus inversiones.
Una varianza alta indica que es probable que los rendimientos reales se desvíen significativamente del valor esperado, lo que hace que la inversión sea más arriesgada, mientras que una varianza baja indica que es probable que los rendimientos reales se acerquen más al valor esperado, lo que hace que la inversión sea menos arriesgada.
Los inversores utilizan la varianza para evaluar y comparar oportunidades de inversión y tomar decisiones informadas sobre sus carteras.