La importancia del valor esperado en el trading

Cada decisión que tome en los mercados financieros debe formularse como un cálculo del valor esperado.

Cada operación o apuesta puede verse como una probabilidad. Existe una probabilidad y una recompensa por acertar y una probabilidad y una penalización por equivocarse.

En otras palabras, la forma de calcular el valor esperado puede explicarse de la siguiente manera:

Valor esperado = P(correcto) * R(correcto) - P(incorrecto) * R(incorrecto)

• P = probabilidad
• R = recompensa

En general, una operación ganadora tendrá un valor esperado positivo, es decir, el valor de la probabilidad de acertar multiplicado por la recompensa por acertar supera a la probabilidad de equivocarse multiplicado por la recompensa por equivocarse. Una operación perdedora tendrá un valor esperado negativo.

Los traders quieren maximizar su valor esperado.

Puntos clave a recordar - Valor esperado

El valor esperado es un concepto estadístico que puede aplicarse al trading. He aquí tres puntos clave que conviene recordar para explicar este concepto:

• El valor esperado es el resultado medio de una estrategia de trading a lo largo de muchas operaciones. Tiene en cuenta la probabilidad de cada resultado y la magnitud del resultado, positivo o negativo.
• Un valor esperado positivo indica que se espera que una estrategia de trading gane dinero a largo plazo, mientras que un valor esperado negativo indica que se espera que una estrategia de trading pierda dinero a largo plazo.
• Al calcular el valor esperado de una estrategia de trading, los traders pueden evaluar si es probable que la estrategia sea rentable o no, y tomar decisiones informadas sobre la gestión del riesgo y el tamaño de las posiciones. Sin embargo, es importante tener en cuenta que el valor esperado no es una garantía de resultados futuros y que los resultados reales de las operaciones pueden diferir del valor esperado.

Ejemplos de valor esperado

Veamos algunos ejemplos de ejercicios.

Ejemplo 1

Supongamos que la probabilidad de acertar es del 70% y la recompensa por acertar es de 50 $, y que la probabilidad de equivocarse es del 30% y la recompensa por equivocarse es de 100 $ (o -100 $ para indicar la pérdida de dinero).

¿Es prudente aceptar esta apuesta?

Siguiendo la fórmula :

• VE = 0.70 * $50 + 0.30 * -$100 = $35 - $30 = +$5.

Dado que el valor esperado es positivo -si ha evaluado correctamente sus probabilidades- la recompensa esperada es mayor que la penalización esperada. Esta apuesta puede ser viable siempre que pueda cubrir la pérdida (-100 $) si se equivoca.

Ejemplo 2

Al comprender el valor esperado, también puede observar que no es prudente apostar sólo por lo que es más probable.

Por ejemplo, en los mercados a menudo encontrará situaciones en las que la probabilidad de acertar es bastante alta, pero la recompensa es baja y la penalización por equivocarse es correspondientemente alta.

Un ejemplo habitual es la venta de opciones out-of-the-money (OTM) sin cobertura. Muchos venderán opciones OTM pensando que sus probabilidades de acertar son altas y que esto hace que la apuesta sea favorable.

Sin embargo, el cálculo real de pérdidas y ganancias suele ser muy diferente.

Si tiene un 90% de probabilidades de acertar y su recompensa es de 20 $, pero tiene un 10% de probabilidades de equivocarse y la penalización es de 1.000 $, la realidad puede ser un poco diferente:

• VE = 0.90 * $20 + 0.10 * $1000 = -$80.

En este caso, puede que tenga un alto porcentaje de ganancias, pero si no hace apuestas de valor esperado positivo, perderá dinero. Y si no puede cubrir la pérdida esperada, existe el elemento de "riesgo de ruina".

Cuando la gente arruina sus cuentas de trading, suele ser por un apalancamiento excesivo, por apostar demasiado en una determinada apuesta en un estilo de todo o nada, o por vender opciones.

La gestión del riesgo es esencial en cualquier circunstancia.

Ejemplo 3

Por otro lado, si sus probabilidades de acertar son bajas pero la recompensa es alta, y si sus probabilidades de equivocarse son altas pero el coste de ese error es insignificante, puede tener sentido hacerlo.

Digamos que tiene un 99% de probabilidades de equivocarse pero el coste de ese error es de 100 dólares, y que tiene un 1% de probabilidades de acertar pero su recompensa es de 100.000 dólares.

Puede ser una apuesta en los mercados financieros o el envío de una solicitud de empleo adicional y la oportunidad de una entrevista, que lleva poco tiempo y no supone pérdida de oportunidades en otro lugar, pero ofrece una recompensa tangible si se acierta, en forma de un salario de calidad, prestaciones y otros beneficios.

• VE = 0,01 * 100.000 $ + 0,99 * -100 $ = +901 $.

Tu recompensa es 1.000 veces mayor que el coste de equivocarte o fracasar y crees que tus posibilidades son tales que tiene sentido arriesgarse, aunque las probabilidades sean aparentemente muy desfavorables.

Si puedes permitirte el coste del error y has evaluado con precisión tus posibilidades, entonces la decisión es muy razonable.

En el trading, el concepto es similar. Si realiza apuestas de valor esperado positivo repetidamente, obtendrá resultados rentables a lo largo del tiempo.

Algunas estrategias que se centran en acontecimientos extremos pueden ser extremadamente rentables en casos excepcionales (por ejemplo, la crisis financiera de 2008, la pandemia de Covid-19 en 2020) y perder muy poco en la mayoría de los demás entornos.

Mark Spitznagel, director de Universa Investments, captó esta idea cuando su empresa ganó más de un 4.000% con coberturas durante la crisis del Covid-19:

"Cuando el mercado se desploma, quiero ganar mucho, y cuando el mercado no se desploma, quiero perder muy poco. Quiero esa asimetría... esa convexidad".

Si está perdiendo dinero y lo está haciendo sobre un tamaño de muestra que hace probable que no esté simplemente lidiando con los caprichos del mercado, entonces realmente necesita evaluar si la estrategia (o estrategias) que está utilizando está poniendo las probabilidades a su favor.

Es importante resistirse a la tentación de creer que perder dinero significa que la suerte no está de su lado.

Ejemplo 4

Si estuvieras jugando a un juego de lanzar una moneda en el que pudieras apostar a cara o cruz, cada una con la misma probabilidad de acertar, ¿arriesgarías 100 $ para ganar 199 $ si aciertas (se devuelven los 100 $ apostados originalmente más 99 $ adicionales) y perderías los 100 $ enteros si te equivocas?

Siguiendo la fórmula :

• VE = 0,50 * 99$ + 0,5 * -100$ = -0,50$.

Así que la respuesta debería ser no.

El valor esperado es sólo ligeramente negativo, por lo que su margen no parece malo.

Sin embargo, si juega a este juego 200 veces con una apuesta igual de 100 $ cada vez, espera perder 100 $ (200 multiplicados por la pérdida esperada de -0,50 $), lo que equivale a su apuesta habitual.

No obstante, todavía hay un 36,7% de posibilidades* de que obtenga beneficios después de 200 tiradas de este juego (harían falta 919 tiradas para que su probabilidad de obtener beneficios bajara a menos del 1%).

* Esta cifra se calcula tomando la ganancia esperada por apuesta, tomando la diferencia en la cantidad apostada por apuesta, y dividiendo por la cantidad apostada por apuesta. Luego se lleva a la potencia del número de rondas jugadas:

[($100 + -$0.50) / $100]^200 = ($99.5/$100)^200 = .995^200 = .367 = 36.7%

Puede llevar un tiempo aprender que tienes una mala estrategia si estás justo en el límite entre algo viable y no mejor que lanzar una moneda al aire.

Ejemplo 5 - Ruleta americana

En una ruleta americana hay 38 números, 18 rojos, 18 negros y 2 verdes.

Si apuestas 10 $ al rojo 10 veces seguidas, ¿qué posibilidades tienes de ganar dinero?

Si aciertas, ganas 20 $ (el doble de tu apuesta), mientras que si te equivocas, lo pierdes todo.

Hay 18 casillas rojas y 38 casillas en total, por lo que su valor esperado por tirada sería :

• VE = 18/38 * 20 $ + 20/38 * 10 $ = 9,47 $.

Esto representa una pérdida esperada de 0,53 $ por tirada (10 $ menos el valor esperado).

¿Cuál es la probabilidad de perder dinero después de 10 rondas?

La probabilidad de perder dinero después de 10 giros, suponiendo que haga apuestas de dinero par en cada giro, se puede calcular utilizando la distribución binomial, que es una fórmula matemática que describe la probabilidad de un cierto número de aciertos en un número fijo de ensayos.

Suponiendo que empiece con una cierta cantidad de dinero y quiera saber la probabilidad de que acabe con menos de esa cantidad después de 10 rondas de apuestas de dinero par, la probabilidad de perder dinero se puede calcular de la siguiente manera:

• P(pérdida) = Σ (i = 0 a 10) (10 elige i) * (47,37%)^i * (52,63%)^(10-i)

Donde "i" representa el número de tiradas que se ganan, "10 pick i" representa el número de formas de elegir "i" tiradas ganadoras de 10, y (47,37%)^i y (52,63%)^(10-i) representan la probabilidad de ganar "i" tiradas y de perder (10-i) tiradas, respectivamente.

Utilizando una calculadora o un programa estadístico, se puede evaluar esta ecuación y ver que la probabilidad de perder dinero después de 10 rondas de apuestas de paridad en la ruleta americana es aproximadamente del 87,9%.

Por lo tanto, las probabilidades de perder dinero después de 10 apuestas de paridad en cada giro en la ruleta americana son bastante altas.

¿Las probabilidades de perder dinero después de 100 giros?

Si continúa haciendo apuestas iguales durante 100 giros de la Ruleta Americana, la probabilidad de perder dinero se puede calcular de la misma manera utilizando la distribución binomial.

La probabilidad de perder dinero después de 100 tiradas se puede calcular de la siguiente manera:

• P(pérdida) = Σ (i = 0 a 100) (100 elige i) * (47,37%)^i * (52,63%)^(100-i)

Utilizando una calculadora o un software estadístico, esta ecuación se puede evaluar para encontrar que la probabilidad de perder dinero después de 100 rondas de apuestas de paridad en la ruleta americana es de alrededor del 99,8%.

Ejemplo 6 - Ruleta Europea

La Ruleta Europea es similar a la Ruleta Americana, pero con una diferencia clave: sólo tiene una casilla 0, mientras que la Ruleta Americana tiene casillas 0 y 00. Esto significa que las probabilidades de ganar una apuesta igualada en la Ruleta Europea son ligeramente mejores que en la Ruleta Americana. Esto significa que las probabilidades de ganar una apuesta igualada en la ruleta europea son ligeramente mejores que en la ruleta americana, ya que hay una casilla menos que da ventaja a la casa.

Suponiendo que haga apuestas pares (por ejemplo, apostar a rojo o negro, par o impar, alto o bajo), las probabilidades de ganar una apuesta individual en la ruleta europea son de 18/37, o aproximadamente el 48,65%. Las probabilidades de perder una apuesta individual son, por tanto, del 51,35%.

Por lo tanto, su VE al apostar al rojo o al negro es :

• VE = 18/37 * 20 $ + 19/37 * 10 $ = 9,73 $.

Por lo tanto, debería esperar perder 0,27 $ por tirada.

Sus probabilidades de ganar dinero en 10 intentos son :

• 1 - ($9.73/$10)^10 = 1 - 0.973^10 = 1 - 0.58 = 0.42 = 42%

Para calcular la probabilidad de perder dinero después de un cierto número de rondas de apuestas iguales en cada giro, podemos utilizar la misma fórmula de distribución binomial que para la ruleta americana.

Suponiendo 10 tiradas de apuestas iguales en la ruleta europea, la probabilidad de perder dinero se puede calcular de la siguiente manera:

• P(pérdida) = Σ (i = 0 a 10) (10 elige i) * (48,65%)^i * (51,35%)^(10-i)

Utilizando una calculadora o un programa estadístico, esta ecuación se puede evaluar para determinar que la probabilidad de perder dinero después de 10 rondas de apuestas pari-mutuel en la ruleta europea es aproximadamente del 83,22%.

Suponiendo 100 rondas de apuestas pari-mutuel en la ruleta europea, la probabilidad de perder dinero se puede calcular de la siguiente manera:

• P(pérdida) = Σ (i = 0 a 100) (100 elige i) * (48,65%)^i * (51,35%)^(100-i)

Utilizando una calculadora o un software estadístico, se puede evaluar esta ecuación para encontrar que la probabilidad de perder dinero después de 100 rondas de apuestas de paridad en la ruleta europea es de aproximadamente el 94,40%.

Por lo tanto, las probabilidades de perder dinero después de 100 tiradas de dinero par en cada giro en la ruleta europea siguen siendo bastante altas, pero ligeramente inferiores a las probabilidades de perder dinero en la ruleta americana.

¿Es siempre mejor centrarse únicamente en el valor esperado?

No, realizar una operación o tomar una decisión de valor esperado positivo (o la operación o decisión de mayor valor esperado) no siempre es la mejor opción.

He aquí algunas razones:

Gestión del riesgo

Una operación o decisión de valor esperado positivo puede conllevar un riesgo significativo.

Los traders deben tener en cuenta no sólo el valor esperado de una operación, sino también el riesgo potencial a la baja, incluida la posibilidad de una gran pérdida.

La gestión del riesgo es una parte importante de cualquier estrategia de trading, y los operadores deben ser capaces de identificar y gestionar el riesgo para minimizar las pérdidas potenciales.

Si tiene una ventaja conocida de 51/49 en algo y puede apostar 10 $ en ello una y otra vez, siempre lo hará si puede. Sin embargo, no querrá comprometer una gran cantidad de dinero en ello porque puede perder varias situaciones 51/49 seguidas.

Coste de oportunidad

Aunque una operación tenga un valor esperado positivo, puede que no sea el mejor uso del capital de un trader.

Si hay otras oportunidades de trading que ofrecen una mejor relación riesgo/recompensa o mayores beneficios potenciales, un trader puede optar por aprovechar estas oportunidades en lugar de la operación de valor esperado positivo.

Situaciones de valor esperado positivo con menor varianza

Supongamos que juegas a un juego con tres opciones:

• Opción 1: 80% de posibilidades de ganar 10.000 dólares.
• Opción 2: 20% de posibilidades de ganar 100.000 $.
• Opción 3: 5% de posibilidades de ganar 1.000.000 $.

Tus valores esperados en cada situación son

• 8,000 $
• 20,000 $
• 50,000 $

¿Qué elegiría la mayoría de la gente en esta situación?

Lo que la mayoría de la gente elegiría en esta situación depende de diversos factores, como su tolerancia al riesgo, su situación financiera y sus objetivos generales.

He aquí algunos escenarios posibles:

• Alto riesgo, alta recompensa: Algunas personas pueden estar dispuestas a asumir más riesgos a cambio de la posibilidad de obtener una alta recompensa. Para estas personas, la opción 3 (5% de posibilidades de ganar 1.000.000 $) puede ser la más atractiva, a pesar de tener una probabilidad menor de ganar. Pueden estar dispuestos a aceptar probabilidades más bajas a cambio de una pequeña posibilidad de obtener una recompensa muy grande y la opción con el valor esperado más alto.
• Riesgo moderado, recompensa moderada: Otras personas pueden ser más reacias al riesgo y preferir un planteamiento más moderado. En este caso, la Opción 2 (20% de posibilidades de ganar 100.000 $) puede resultar más atractiva. Aunque el valor esperado es inferior al de la Opción 3, la probabilidad de ganar es mayor, lo que la convierte en una opción de riesgo-recompensa más moderado.
• Riesgo bajo, recompensa baja: Para las personas con gran aversión al riesgo o recursos financieros limitados, la Opción 1 (80% de probabilidades de ganar 10.000 $) puede ser la más atractiva. Aunque el valor esperado es inferior al de las opciones 2 y 3, la probabilidad de ganar es mucho mayor, lo que la convierte en una opción más segura con una recompensa menor.

En los mercados, esto podría ser análogo a elegir entre bonos seguros, acciones o inversiones especulativas de nueva creación.

Las probabilidades son dinámicas y a menudo desconocidas

Las probabilidades no suelen conocerse explícitamente y rara vez son estáticas.

El mercado puede ser impredecible, y factores como noticias inesperadas o cambios en el sentimiento del mercado pueden alterar rápidamente el valor esperado de una operación.

Los traders deben ser capaces de adaptarse a las condiciones cambiantes del mercado y ajustar sus estrategias en consecuencia.

Costes de trading

Realizar una operación con un valor esperado positivo no garantiza obtener beneficios, ya que los costes de trading, como las comisiones, las tasas y los diferenciales, pueden reducir los beneficios potenciales.

Los traders deben tener en cuenta estos costes al calcular el valor esperado de una operación y ajustar sus estrategias en consecuencia.

En resumen, aunque en general se favorecen las operaciones o decisiones de valor esperado positivo, los traders deben tener en cuenta otros factores como la gestión del riesgo, el coste de oportunidad, las condiciones del mercado y los costes de negociación a la hora de tomar decisiones. El trading es un proceso complejo y dinámico, y los traders deben ser capaces de adaptarse a las condiciones cambiantes del mercado y tomar decisiones informadas en función de diversos factores.

Valor esperado en el trading con opciones

El valor esperado se utiliza a menudo en el trading con opciones, en particular.

A muchos traders les gustan las opciones porque les permiten captar una parte específica de la distribución de resultados potenciales. Esto significa que pueden adaptar más cuidadosamente sus ideas de negociación y sus tesis de inversión para expresar determinados puntos de vista.

Para saber si merece la pena realizar una operación, es importante realizar cálculos del valor esperado.

Tendrá resultados potenciales que conocerá de antemano en función de cómo estructure la operación.

Entonces tendrá que asignar probabilidades a cada resultado para determinar el valor esperado de cada elemento. Al sumarlos, obtendrá el valor esperado de toda la operación.

Brokers de opciones

Brokers	Reglamentación	Plataformas	Depósito mínimo	Tipos de opciones
	Irlanda (FRSA)	AvaOptions	100 €	Opciones sobre divisas (OTC)
Invertir implica el riesgo de sufrir pérdidas. Los contratos de opciones son productos financieros complejos diseñados para inversores experimentados.

Ejemplo

Supongamos que desea colocar una opción de compra cubierta sobre una acción, tomando el vencimiento más próximo en una semana. Para estar seguro, también quiere limitar sus pérdidas si el precio de las acciones cae, por lo que también compra opciones de venta.

Supongamos que las acciones cotizan a 54 $ cada una. Supongamos que quiere comprar 1.000 acciones.

Quiere maximizar la prima de riesgo de volatilidad que saca del mercado, por lo que suscribe opciones de compra con un precio de ejercicio de 54 $.

Para estar a la defensiva si la acción cae, también compra opciones de venta con un precio de ejercicio de 52. Esto limita sus pérdidas potenciales a 2 $ por acción. Esto limita sus pérdidas potenciales a 2 $ por acción.

La estructura de su operación es esencialmente un tipo de collar que se parece al diagrama siguiente, con un punto de equilibrio en algún punto intermedio.

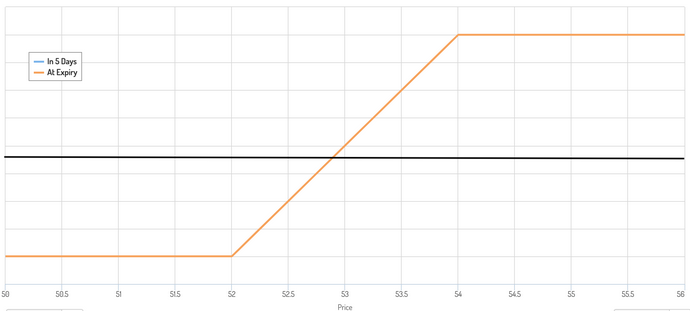
Posibles resultados

Tiene tres resultados categóricos en cuanto al resultado final:

• Operar por encima del límite superior del collar (es decir, por encima de 54 $ por acción).
• Operar dentro del collar (es decir, entre 52 y 54 dólares por acción).
• Operar por debajo del límite inferior del collar (es decir, por debajo de 52 $ por acción).

Dado que el límite superior del collar es donde el precio está cotizando actualmente, estar por encima del límite superior de la banda es el más probable de estos tres escenarios.

Como se trata de un periodo semanal, las probabilidades de terminar por encima de la banda son de aproximadamente el 50%.

También podemos decir que operar dentro del collar (0-3,7% out-of-the-money (OTM)) tiene aproximadamente un 33% de posibilidades, basándonos en lo que implica el precio de la opción.

Algunos brokers (por ejemplo, Interactive Brokers con su función "Probability Lab") ponen a su disposición estas herramientas.

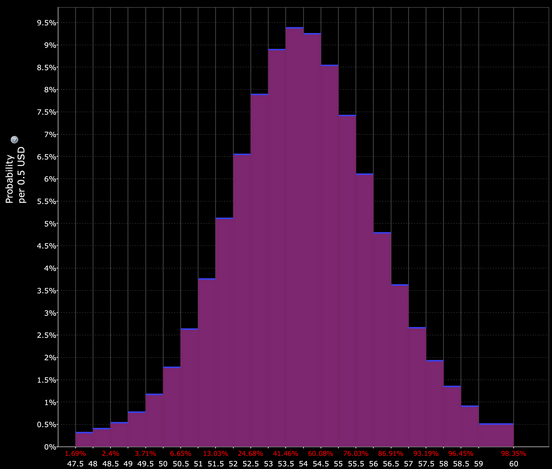
Esto significa que la operación por debajo del límite inferior del collar (52 $ y por encima) tiene aproximadamente un 17% de posibilidades.

¿Cómo se calcula el valor esperado de esta estructura de negociación?

Para calcular los valores esperados asociados a los escenarios "por encima del límite superior" y "por debajo del límite inferior", basta con tomar el coste de la opción y el movimiento de la acción correspondiente.

Para determinar el valor esperado de la categoría intermedia, podemos simplemente tomar el punto medio del precio y basarnos en él (en este caso, 53 $ por acción).

Ganancia/pérdida "por encima del límite superior"

Para el "límite superior", el valor esperado es simplemente el crédito que obtenemos por vender las 54 opciones de compra.

Como compramos 1.000 acciones y hay 100 acciones por contrato de opción, son 10 contratos. Se vendían a 94 $ por contrato (0,94 $ por acción) por un total de 940 $.

El coste de las 52 opciones de venta era de 29 $ por contrato (0,29 $ por acción), lo que supone un total de 290 $.

Restamos los dos, 940 $ menos 290 $, para +650 $.

Ganancia/pérdida "por debajo del límite inferior

En este caso, seguimos obteniendo el beneficio neto de 650 $ de las opciones.

Sin embargo, si caemos por debajo de 54 $, incurrimos en pérdidas de capital sobre las acciones. La compra de las opciones de venta de 52 limita las pérdidas a 2 $ por acción (54 $ menos 52 $). Para 1.000 acciones, son 2.000 $.

Así que ganamos 650 $ de nuestro beneficio menos 2.000 $, lo que supone una pérdida de 1.350 $.

Ganancia/pérdida "dentro del collar

En este caso, tomamos el punto medio (53 $ al vencimiento).

Aquí tenemos una pérdida de capital de 1 $ por acción. Con 1.000 acciones, son 1.000 $.

Ganamos 650 $ del beneficio neto de las opciones y restamos los 1.000 $ (la pérdida) para una pérdida neta de 350 $.

¿Cuál es nuestro valor esperado?

Multiplicamos nuestras ganancias/pérdidas individuales por la probabilidad de que se produzcan.

Esto nos da :

• Por encima del límite superior: 650 $ * 0,50 = 325 $.
• Por debajo del límite superior: -1350 $ * 0,17 = -229,50 $.
• Dentro del collar: -350 $ * 0,33 = -115,50 $.

Sumamos estos valores y obtenemos -20 $ para el valor esperado.

Por lo tanto, si evaluáramos nuestras probabilidades como tales, no tendríamos un valor esperado positivo.

Tendría sentido que esta cifra estuviera cerca del punto de equilibrio, ya que estamos utilizando en gran medida probabilidades aproximadas sugeridas por el mercado.

Esto ilustra otra realidad: para ganar dinero en los mercados (más allá de un valor de referencia), hay que apostar en contra del consenso y acertar.

Si pensáramos que las probabilidades asociadas a cada una de ellas son, en cambio, de 0,52, 0,15 y 0,33, entonces nuestro valor esperado sería positivo: 20 $.

Otros factores en el cálculo del valor esperado

Es especialmente importante incluir los costes de transacción.

No se trata sólo del coste de la operación, sino también de la diferencia entre lo que se negocia y la calidad de la ejecución.

También incluyen los costes de financiación y/o los costes de endeudamiento.

Muchos valores y mercados no cuentan con mercados de opciones de gran liquidez, lo que significa que el diferencial suele ser bastante grande y que hay una falta de tamaño en los precios de compra y venta.

Esto es especialmente importante para las grandes instituciones y las grandes cuentas, en general. Los costes de transacción tienden a aumentar de forma no lineal.

Los costes de transacción también pueden influir en lo que usted quiere negociar.

Por ejemplo, si negocia con bonos de duración media a larga, los contratos de futuros ZB incluyen entre 150.000 y 200.000 dólares de bonos por contrato, dependiendo del precio exacto. Esto significa que puede comprar un único contrato de opción para futuros ZB, mientras que necesita comprar unos 11 contratos para una cantidad equivalente de TLT (un equivalente del ETF de bonos de mayor duración).

Los intermediarios suelen cobrar en función del volumen de contratos. Las opciones sobre contratos de futuros suelen tener un precio más elevado que las opciones sobre acciones y ETF. Pero los contratos de futuros suelen incluir un mayor volumen del subyacente por contrato, lo que puede ayudarle a reducir algunos gastos si el tamaño es adecuado para su cartera.

Pasar de lo intuitivo a lo explícito

Aunque no hagas conscientemente cálculos de valor esperado, los haces intuitivamente todo el tiempo.

Si tiene que coger un vuelo, probablemente salga hacia el aeropuerto con bastante antelación para disponer de un margen de tiempo razonable.

De ese modo, es prácticamente imposible perder el vuelo si hay problemas en el aeropuerto, largas colas, un retraso en el control de seguridad, un billete o pasaporte extraviado o cualquier otra cosa que pueda reducir ese tiempo.

Lo haces porque el inconveniente de perder un vuelo es alto en términos de coste monetario, molestias y/o pérdida de oportunidades.

Otra forma de calcular el valor esperado es no conducir con exceso de velocidad. Si las probabilidades de que le pongan una multa por exceso de velocidad son bastante bajas si apenas sobrepasa el límite de velocidad, puede optar por no conducir si el riesgo de que le pongan una multa es demasiado alto (es decir, una multa, tiempo perdido al ser parado y posiblemente más).

El trading no es muy diferente de los escenarios de la vida real a los que nos enfrentamos y que hacemos para maximizar nuestra utilidad y limitar nuestro riesgo.

Asumir un riesgo cuando se tiene mucho que ganar y muy poco que perder (por ejemplo, oportunidades de empleo) es muy parecido a operar en situaciones en las que se tiene un lado negativo limitado y un lado positivo teóricamente ilimitado (por ejemplo, comprando opciones OTM baratas).

Del mismo modo, es mejor ser precavido cuando la pérdida es muy grande, aunque las probabilidades sean pequeñas (por ejemplo, un chequeo médico si se padece un determinado síntoma). Esto es similar a los traders que venden opciones out-of-the-money (OTM) por una prima muy baja.

Cuando se produce el evento de baja probabilidad, pierden muchas veces la prima que esperaban recibir (a veces cientos o incluso más).

A medida que los operadores adquieren experiencia y sabiduría, están menos dispuestos y son menos propensos a negociar cosas sobre las que no tienen fuertes convicciones.

Irónicamente, los traders novatos tienden a estar bastante seguros de sí mismos y listos para lanzarse, mientras que los traders experimentados son los que más temen equivocarse, debido a su exposición a los mercados a lo largo del tiempo y a los inevitables episodios dolorosos que les han seguido.

Todos los operadores deben ser conscientes de la gravedad de la situación y del margen de mejora que tienen. Esta es la razón por la que algunos operadores optan por no ponerse nunca cortos en gamma (lo que básicamente significa que nunca venden opciones).

Aunque esta filosofía lleva a algunos a no aprovechar nunca una fuente de rentabilidad conocida como prima de riesgo de volatilidad, saben que si nunca se ponen cortos en gamma, nunca podrán explotar. Para algunos, es una cuestión de gestión prudente del riesgo.

Los traders tienden a basarse en el pasado reciente para predecir el futuro. Pueden ocurrir cosas que no están en su distribución y no se pueden poner en precio.

Si algo no ha ocurrido nunca, la única forma de protegerse contra lo desconocido es eliminar por completo el riesgo de cola. Por lo tanto, muchos operadores muy avanzados en la comprensión del riesgo y la recompensa intentarán estructurar sus operaciones utilizando opciones.

Si venden opciones, las cubren con una posición en el subyacente o con otro tramo de la estructura de opciones. Al comprar opciones, la gestión del riesgo recae enteramente sobre los hombros de la contraparte (es decir, la persona que le ha vendido la opción).

Esto también facilita los cálculos del valor esperado, ya que se tiene un riesgo negativo claramente definido.

Además, para quienes establecen stop-losses, los mercados se desploman cuando se cierran a la negociación activa durante un periodo de tiempo o cuando se produce una perturbación, un acontecimiento importante o un dato. Un stop-loss no mitigará el riesgo durante periodos anormales.

Conclusión

Si es usted trader, jugador profesional o cualquier otro tipo de profesional de la toma de decisiones, es esencial que conozca el concepto de valor esperado.

Los mercados son similares al póquer. Debe evaluar constantemente sus posibilidades de acertar, su recompensa por acertar, las posibilidades y la penalización por equivocarse, y cómo evaluar esta información con un conocimiento que casi siempre es imperfecto.

Para tomar las mejores decisiones de trading, hay que entender el riesgo y la recompensa.

¿Cuál es su riesgo, cuánto puede ganar al alza y, lo que es muy importante, cuáles son las probabilidades de que estas cosas ocurran?

No es un proceso fácil. Para los distintos operadores significa cosas distintas.

Algunos quieren saber explícitamente cuál es su riesgo a la baja mediante opciones largas o una gestión estricta del riesgo en forma de stop-loss.

Saben que hay dos tipos de riesgo bajo control: (1) cuánto pueden perder y (2) que el "riesgo de ruina" es imposible (siempre pueden cubrir la pérdida).

Los mejores traders limitan las pérdidas cuando se equivocan y obtienen grandes beneficios cuando aciertan.

Utilizando una analogía del béisbol, lo que cuenta no es tu media de bateo (la proporción de bateos acertados con respecto al total de bateos), sino tu porcentaje de victorias (la calidad general de los bateos o la cantidad producida cuando aciertas).

Apostar por lo que es más probable no siempre es lo mejor cuando los operadores entienden el valor esperado.

Demasiados aspiran a "victorias fáciles" -por ejemplo, vendiendo opciones OTM- y acaban anulando el beneficio de un montón de pequeñas ganancias con lo que ocurre cuando inevitablemente una de ellas fracasa, y a menudo por varias veces.

Brokers de CFD

CFD Brokers	Plataformas	Regulado por la	Abrir una cuenta de demostración
	xStation 5	FCA, KNF, CySEC, BIFSC, CNMV, DFSA
	MetaTrader 4 y 5	CySEC, FCA, ASIC, JSC, OCRCVM, FSCA
	MetaTrader 4 y 5	ASIC, CBFSAI, FRSA, BVI FSC, FSCA, JFSA, OCRCVM
ASIC: Australia, BaFin: Alemania, BIFSC: Belice, BVI FSC: Islas Vírgenes Británicas, BACEN & CVM: Brasil, CySEC: Chipre, CNMV: España, CMVM: Portugal, CSSF: Luxemburgo, CFTC: EE.UU., CBFSAI: Irlanda, CMA: Omán,, DFSA: Dubai, FCA: Reino Unido, FINMA: Suiza, FSPR - FMA: Nueva Zelanda, FRSA: Abu Dhabi, FSA: Seychelles, FSCA: Sudáfrica, JFSA: Japón, JSC: Jordania, KNF: Polonia, MAS: Singapur, OCRCVM: Canadá, SCB: Bahamas, VFSC: Vanuatu.
Las operaciones con CFDs implican un importante riesgo de pérdida, por lo que no son adecuadas para todos los inversores. Entre el 74 y el 89% de las cuentas de los inversores minoristas pierden dinero al operar con CFD.