A importância do valor esperado no trading

Cada decisão que tomar nos mercados financeiros deve ser formulada como um cálculo do valor esperado.
Cada transacção ou aposta pode ser vista como uma probabilidade. Há uma probabilidade e uma recompensa por estar certo e uma probabilidade e uma penalidade por estar errado.
Por outras palavras, a forma de calcular o valor esperado pode ser explicada como se segue:
Valor esperado = P(correcto) * R(correcto) - P(incorrecto) * R(incorrecto)
- P = probabilidade
- R = recompensa
Em geral, um negócio vencedor terá um valor esperado positivo, ou seja, o valor da probabilidade de estar certo multiplicado pela recompensa por estar certo excede a probabilidade de estar errado multiplicado pela recompensa por estar errado. Uma troca perdedora terá um valor esperado negativo.
Os traders querem maximizar o seu valor esperado.
Pontos-chave a lembrar - Valor esperado
O valor esperado é um conceito estatístico que pode ser aplicado ao trading. Aqui estão três pontos-chave a lembrar para explicar este conceito:
- O valor esperado é o resultado médio de uma estratégia de trading em muitas transacções. Tem em conta a probabilidade de cada resultado e a magnitude do resultado, positivo ou negativo.
- Um valor esperado positivo indica que se espera que uma estratégia de trading ganhe dinheiro a longo prazo, enquanto um valor esperado negativo indica que se espera que uma estratégia de trading perca dinheiro a longo prazo.
- Ao calcular o valor esperado de uma estratégia de trading, os traders podem avaliar se a estratégia é ou não rentável, e tomar decisões informadas sobre a gestão do risco e o dimensionamento da posição. No entanto, é importante notar que o valor esperado não é uma garantia de resultados futuros e que os resultados reais da trading podem diferir do valor esperado.
Exemplos de valor esperado
Vejamos alguns exemplos de exercícios.
Exemplo 1
Suponha que a probabilidade de estar certo é de 70% e a recompensa por estar certo é de $50, e a probabilidade de estar errado é de 30% e a recompensa por estar errado é de $100 (ou -$100 para indicar a perda de dinheiro).
Será sensato aceitar esta aposta?
Seguindo a fórmula :
- VE = 0,70 * $50 + 0,30 * -$100 = $35 - $30 = +$5.
Uma vez que o valor esperado é positivo - se tiver avaliado correctamente as suas probabilidades - a recompensa esperada é maior do que a penalização esperada. Esta aposta pode ser viável desde que possa cobrir a perda (-$100) se estiver errado.
Exemplo 2
Ao compreender o valor esperado, também se pode observar que não é sensato apostar apenas no que é mais provável.
Por exemplo, nos mercados, encontrará frequentemente situações em que a probabilidade de estar certo é bastante elevada, mas a recompensa é baixa e a penalização por estar errado é correspondentemente elevada.
Um exemplo comum disto é a venda de opções de venda a descoberto fora do dinheiro (OTM). Muitos venderão opções OTM pensando que as suas probabilidades de estarem certos são altas e que isto torna a aposta favorável.
No entanto, o cálculo real dos lucros e perdas é muitas vezes muito diferente.
Se tiver 90% de hipóteses de estar certo e a sua recompensa for de $20, mas tiver 10% de hipóteses de estar errado e a penalização for de $1,000, a realidade pode ser um pouco diferente:
- VE = 0,90 * $20 + 0,10 * $1000 = -$80.
Neste caso, pode ter uma elevada percentagem de ganho, mas se não fizer apostas de valor esperado positivo, perderá dinheiro. E se não conseguir cobrir a perda esperada, existe o elemento "risco de ruína".
Quando as pessoas arruínam as suas contas de trading, é normalmente devido à alavancagem excessiva, apostar demasiado numa determinada aposta num estilo tudo ou nada, ou vender opções.
A gestão do risco é essencial em todas as circunstâncias.
Exemplo 3
Por outro lado, se as suas hipóteses de estar certo são baixas mas a recompensa é alta, e se as suas hipóteses de estar errado são altas mas o custo desse erro é insignificante, pode fazer sentido fazê-lo.
Digamos que tem 99% de hipóteses de estar errado, mas o custo desse erro é de $100, e tem 1% de hipóteses de estar certo, mas a sua recompensa é de $100.000.
Isto pode ser uma aposta nos mercados financeiros ou o envio de uma candidatura a um emprego adicional e a oportunidade de entrevista, o que leva pouco tempo e nenhuma perda de oportunidade noutros locais, mas oferece uma recompensa tangível se for bem sucedido, sob a forma de um salário de qualidade, benefícios e outras regalias.
- VE = 0,01 * $100.000 + 0,99 * -$100 = +$901
A sua recompensa é 1.000 vezes maior do que o custo de estar errado ou falhar e sente que as suas hipóteses são tais que faz sentido arriscar, mesmo que as probabilidades sejam aparentemente muito desfavoráveis.
Se puder suportar o custo do erro e tiver avaliado correctamente as suas hipóteses, então a decisão é muito razoável.
No trading, o conceito é semelhante. Se fizer apostas de valor positivo esperado repetidamente, obterá resultados rentáveis ao longo do tempo.
Algumas estratégias que se concentram em eventos extremos podem ser extremamente rentáveis em casos raros (por exemplo, a crise financeira de 2008, a pandemia de Covid-19 em 2020) e perder muito pouco na maioria dos outros ambientes.
Mark Spitznagel, director da Universa Investments, captou esta ideia quando a sua empresa ganhou mais de 4,000% ao fazer cobertura durante a crise do Covid-19:
"Quando o mercado cai, eu quero fazer muito, e quando o mercado não cai, quero perder uma quantidade muito pequena. Quero essa assimetria... essa convexidade".
Se estás a perder dinheiro e o estás a fazer por cima de uma amostra de tamanho que torna provável que não estejas apenas a lidar com os caprichos do mercado, então precisas realmente de avaliar se a estratégia (ou estratégias) que estás a usar está a colocar as probabilidades a teu favor.
É importante resistir à tentação de acreditar que perder dinheiro significa que a sorte não está do seu lado.
Exemplo 4
Se estivesse a jogar um jogo de atirar moedas onde pudesse apostar em cabeças ou caudas, cada um com as mesmas hipóteses de estar correcto, arriscaria 100 dólares para ganhar 199 dólares se estivesse certo (a aposta original de 100 dólares é reembolsada mais 99 dólares no topo) e perder os 100 dólares inteiros se estivesse errado?
Seguindo a fórmula :
- VE = 0,50 * $99 + 0,5 * -$100 = -$0,50.
Portanto, a resposta deve ser não.
O valor esperado é apenas ligeiramente negativo, pelo que a sua margem não parece má.
Contudo, se jogar este jogo 200 vezes com uma aposta igual de $100 cada vez, espera perder $100 (200 multiplicados pela perda esperada de -$0,50), o que é equivalente à sua aposta habitual.
No entanto, existe ainda uma probabilidade de 36,7%* de ser rentável após 200 rodadas deste jogo (seriam necessárias 919 rodadas para que a sua probabilidade de ser rentável descesse para menos de 1%).
* Este número é calculado tomando o ganho esperado por aposta, tomando a diferença no montante apostado por aposta, e dividindo pelo montante apostado por aposta. Depois é levado à potência do número de rondas jogadas:
[($100 + -$0.50) / $100]^200 = ($99.5/$100)^200 = .995^200 = .367 = 36.7%
Pode demorar algum tempo a aprender que tem uma má estratégia se estiver apenas na fronteira entre algo viável e não melhor do que atirar uma moeda ao ar.
Ejemplo 5 - Ruleta americana
En una ruleta americana hay 38 números, 18 rojos, 18 negros y 2 verdes.
Si apuestas 10 $ al rojo 10 veces seguidas, ¿qué posibilidades tienes de ganar dinero?
Si aciertas, ganas 20 $ (el doble de tu apuesta), mientras que si te equivocas, lo pierdes todo.
Hay 18 casillas rojas y 38 casillas en total, por lo que su valor esperado por tirada sería :
- VE = 18/38 * 20 $ + 20/38 * 10 $ = 9,47 $.
Esto representa una pérdida esperada de 0,53 $ por tirada (10 $ menos el valor esperado).
¿Cuál es la probabilidad de perder dinero después de 10 rondas?
La probabilidad de perder dinero después de 10 giros, suponiendo que haga apuestas de dinero par en cada giro, se puede calcular utilizando la distribución binomial, que es una fórmula matemática que describe la probabilidad de un cierto número de aciertos en un número fijo de ensayos.
Suponiendo que empiece con una cierta cantidad de dinero y quiera saber la probabilidad de que acabe con menos de esa cantidad después de 10 rondas de apuestas de dinero par, la probabilidad de perder dinero se puede calcular de la siguiente manera:
- P(pérdida) = Σ (i = 0 a 10) (10 elige i) * (47,37%)^i * (52,63%)^(10-i)
Onde "i" representa o número de rotações que ganha, "10 pick i" representa o número de formas de escolher "i" rotações vencedoras de 10, e (47,37%)^i e (52,63%)^(10-i) representam a probabilidade de ganhar "i" rotações e perder (10-i) rotações, respectivamente.
Usando uma calculadora ou software estatístico, pode-se avaliar esta equação e ver que a probabilidade de perder dinheiro após 10 rodadas de apostas de paridade na roleta americana é de aproximadamente 87,9%.
Portanto, as probabilidades de perder dinheiro depois de 10 rodadas de apostas iguais em cada rodada na Roleta Americana são bastante elevadas.
As probabilidades de perder dinheiro depois de 100 rodadas?
Se continuar a fazer apostas de igual valor para 100 rodadas da Roleta Americana, a probabilidade de perder dinheiro pode ser calculada da mesma forma, utilizando a distribuição binomial.
A probabilidade de perder dinheiro depois de 100 rodadas pode ser calculada da seguinte forma:
- P(perda) = Σ (i = 0 a 100) (100 escolher i) * (47,37%)^i * (52,63%)^(100-i)
Usando uma calculadora ou software estatístico, esta equação pode ser avaliada para descobrir que a probabilidade de perder dinheiro após 100 rondas de apostas de paridade na roleta americana é de cerca de 99,8%.
Exemplo 6 - Roleta Europeia
A Roleta Europeia é semelhante à Roleta Americana, mas com uma diferença chave: tem apenas um bolso 0, enquanto que a Roleta Americana tem ambos os bolsos 0 e 00. Isto significa que as probabilidades de ganhar uma aposta equilibrada na roleta europeia são ligeiramente melhores do que na roleta americana, já que há menos um bolso que dá uma vantagem à casa.
Assumindo que se fazem apostas pares (por exemplo, apostando no vermelho ou no preto, ímpares ou pares, altas ou baixas), as probabilidades de ganhar uma aposta individual na roleta europeia são de 18/37, ou cerca de 48,65%. As probabilidades de perder uma aposta individual são, portanto, de cerca de 51,35%.
Assim, o seu VE ao apostar no vermelho ou no preto é :
- VE = 18/37 * $20 + 19/37 * $10 = $9,73.
Portanto, deve esperar perder $0,27 por rodada.
As suas hipóteses de ganhar dinheiro em 10 tentativas são :
- 1 - ($9.73/$10)^10 = 1 - 0.973^10 = 1 - 0.58 = 0.42 = 42%
Para calcular a probabilidade de perder dinheiro após um certo número de rondas de apostas iguais em cada rodada, podemos utilizar a mesma fórmula de distribuição binomial que para a roleta americana.
Assumindo 10 rodadas de apostas iguais na roleta europeia, a probabilidade de perda de dinheiro pode ser calculada da seguinte forma:
- P(perda) = Σ (i = 0 a 10) (10 escolha i) * (48,65%)^i * (51,35%)^(10-i)
Usando uma calculadora ou software estatístico, esta equação pode ser avaliada para determinar que a probabilidade de perder dinheiro após 10 rondas de apostas pari-mutuel na roleta europeia é de aproximadamente 83,22%.
Assumindo 100 rondas de apostas paritárias na roleta europeia, a probabilidade de perda de dinheiro pode ser calculada da seguinte forma:
- P(perda) = Σ (i = 0 a 100) (100 escolher i) * (48,65%)^i * (51,35%)^(100-i)
Usando uma calculadora ou software estatístico, pode-se avaliar esta equação para descobrir que a probabilidade de perder dinheiro após 100 rondas de apostas de paridade na roleta europeia é de aproximadamente 94,40%.
Portanto, as probabilidades de perder dinheiro após 100 rodadas de paridade em cada rodada na roleta europeia são ainda bastante elevadas, mas ligeiramente inferiores às probabilidades de perder dinheiro na roleta americana.
É sempre melhor concentrar-se apenas no valor esperado?
Não, tomar uma decisão ou comércio de valor esperado positivo (ou o comércio ou decisão de maior valor esperado) nem sempre é a melhor escolha.
Eis algumas razões para tal:
Gestão do risco
Um comércio ou decisão de valor esperado positivo ainda pode comportar um risco significativo.
Os traders devem considerar não só o valor esperado de uma transacção mas também o potencial risco de perda, incluindo a possibilidade de uma grande perda.
A gestão do risco é uma parte importante de qualquer estratégia de trading, e os traders devem ser capazes de identificar e gerir o risco para minimizar perdas potenciais.
Se tiver uma vantagem conhecida de 51/49 em algo e puder apostar $10 vezes sem conta, fá-lo-á sempre se puder. No entanto, não quer comprometer uma grande quantia de dinheiro porque pode perder várias situações 51/49 seguidas.
Custo da oportunidade
Mesmo que um comércio tenha um valor esperado positivo, pode não ser a melhor utilização do capital de um trader.
Se existirem outras oportunidades de trading que ofereçam uma melhor relação risco/retorno ou lucros potenciais mais elevados, um trader pode optar por aproveitar estas oportunidades em vez da transacção de valor positivo esperado.
Situações de Valor Esperado Positivo com Menor Variação
Digamos que se joga um jogo com três opções:
- Opção 1: 80% de hipóteses de ganhar $10.000.
- Opção 2: 20% de probabilidades de ganhar $100.000.
- Opção 3: 5% de probabilidades de ganhar $1.000.000.
Os seus valores esperados em cada situação são
- 8,000 $
- 20,000 $
- 50,000 $
O que é que a maioria das pessoas escolheria nesta situação?
O que a maioria das pessoas escolheria nesta situação depende de uma variedade de factores, incluindo a sua tolerância ao risco, situação financeira e objectivos gerais.
Aqui estão alguns cenários possíveis:
- Risco elevado, recompensa elevada: Algumas pessoas podem estar dispostas a correr mais riscos em troca de uma oportunidade de recompensa elevada. Para estas pessoas, a Opção 3 (5% de probabilidade de ganhar $1.000.000) pode ser a mais atractiva, apesar de uma menor probabilidade de ganhar. Podem estar dispostas a aceitar probabilidades mais baixas em troca de uma pequena probabilidade de um pagamento muito grande e a opção com o maior valor esperado.
- Risco moderado, recompensa moderada: Outras pessoas podem ser mais avessas ao risco e preferir adoptar uma abordagem mais moderada. Neste caso, a Opção 2 (20% de probabilidade de ganhar $100.000) pode ser mais atractiva. Embora o valor esperado seja inferior ao da Opção 3, a probabilidade de ganhar é maior, tornando-a uma opção mais moderada de risco-retorno.
- Risco baixo, baixa recompensa: Para aqueles com aversão ao risco elevado ou recursos financeiros limitados, a Opção 1 (80% de probabilidade de ganhar $10.000) pode ser a mais atractiva. Embora o valor esperado seja inferior às Opções 2 e 3, a probabilidade de ganhar é muito maior, tornando-a uma opção mais segura com uma recompensa menor.
Nos mercados, isto poderia ser análogo à escolha entre obrigações seguras, acções ou investimentos especulativos de arranque.
As probabilidades são dinâmicas e muitas vezes desconhecidas
As probabilidades não são muitas vezes explicitamente conhecidas e raramente são estáticas.
O mercado pode ser imprevisível, e factores tais como notícias inesperadas ou mudanças no sentimento do mercado podem rapidamente alterar o valor esperado de uma transacção.
Os traders devem ser capazes de se adaptar às condições de mercado em mudança e ajustar as suas estratégias em conformidade.
Custos de trading
Fazer um comércio de valor esperado positivo não garante um lucro, uma vez que custos de trading como comissões, taxas e spreads podem reduzir potenciais lucros.
Os traders devem ter estes custos em conta ao calcular o valor esperado de uma transacção e ajustar as suas estratégias em conformidade.
Em resumo, embora as negociações ou decisões de valor esperado positivo sejam geralmente favorecidas, os traders devem considerar outros factores, tais como gestão de risco, custo de oportunidade, condições de mercado e custos de trading ao tomarem decisões. A negociação é um processo complexo e dinâmico, e os negociadores devem ser capazes de se adaptar às condições de mercado em mudança e tomar decisões informadas com base em vários factores.
Valor esperado no trading de opções
O valor esperado é frequentemente utilizado no trading de opções, em particular.
Muitos traders gostam de opções porque lhes permitem captar uma parte específica da distribuição de resultados potenciais. Isto significa que podem adaptar mais cuidadosamente as suas ideias comerciais e teses de investimento para expressar certos pontos de vista.
Para saber se vale a pena fazer uma transacção, é importante efectuar os cálculos do valor esperado.
Terá resultados potenciais que conhece antecipadamente, dependendo de como estruturar o comércio.
Terá então de atribuir probabilidades a cada resultado para determinar o valor esperado de cada item. Ao somá-las, obterá o valor esperado para todo o comércio.
Brokers de opções
Exemplo
Suponha que você queira colocar uma opção de compra coberta em uma ação, tendo os vencimentos mais próximos dentro de uma semana. Para estar no lado seguro, você também deseja limitar suas perdas se os preços das ações caírem, então você também compra opções de venda.
Digamos que as ações estejam sendo negociadas a US$ 54 cada. Suponha que você queira comprar 1.000 ações.
Você queria maximizar o prêmio de risco de volatilidade obtido do mercado, então você vende opções de compra com um preço de exercício de 54.
Para ficar na defensiva quando a ação cair, você também compra opções de venda com um preço de exercício de 52. Isso limita suas perdas potenciais a US$ 2 por ação.
Sua estrutura comercial é essencialmente um tipo de colar que se parece com o diagrama abaixo, com um ponto de equilíbrio em algum lugar no meio.
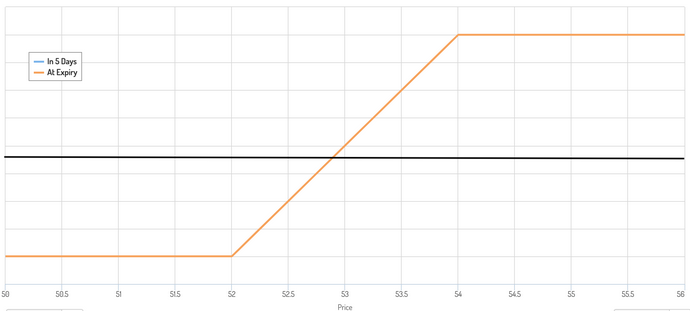
Potenciais resultados
Tem três resultados categóricos em termos do resultado final:
- Transacção acima do limite superior do colar (ou seja, acima de $54 por acção).
- Transacção dentro do colar (ou seja, entre $52 e $54 por acção)
- Transacção abaixo do limite inferior do colar (ou seja, abaixo de $52 por acção).
Uma vez que o limite superior do colar é onde o preço é actualmente negociado, estar acima do limite superior do colarinho é o mais provável destes três cenários.
Como este é um período semanal, as suas hipóteses de terminar acima da faixa são de cerca de 50%.
Podemos também dizer que o trading dentro do colarinho (0-3,7% out-of-the-money (OTM)) tem cerca de 33% de hipóteses, com base no que o preço da opção implica.
Alguns brokers (por exemplo, Interactive Brokers com o seu "Laboratório de Probabilidade") disponibilizam-lhe estas ferramentas.
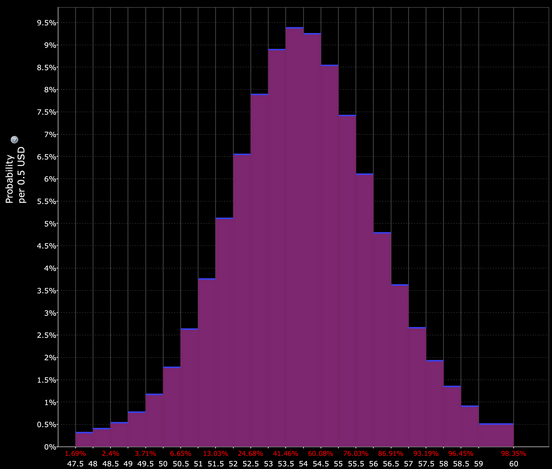
Isto significa que o comércio abaixo do colar inferior ($52 e acima) tem cerca de 17% de hipóteses.
Como se calcula o valor esperado desta estrutura comercial?
Para calcular os valores esperados associados aos cenários "acima do limite superior" e "abaixo do limite inferior", tomamos simplesmente o custo da opção e o movimento de stock relevante.
Para determinar o valor esperado da categoria intermédia, podemos simplesmente tomar o ponto médio do preço e baseá-lo nisso (neste caso, $53 por acção).
Ganho/perda "acima do limite superior".
Para o "limite superior", o valor esperado é simplesmente o crédito que obtemos pela venda das 54 chamadas.
Uma vez que comprámos 1.000 acções e há 100 acções por contrato de opção, são 10 contratos. Foram vendidos por $94 por contrato ($0,94 por acção) por um total de $940.
O custo das 52 puts foi de $29 por contrato ($0,29 por acção), para um total de $290.
Subtraímos os dois, $940 menos $290, por +$650.
Ganho/perda "abaixo do limite inferior
Neste caso, ainda obtemos os $650 de lucro líquido das opções.
No entanto, se formos abaixo dos 54 dólares, incorremos em perdas de capital sobre as acções. Se formos para os 52, as perdas são limitadas a $2 por acção ($54 menos $52). Para 1.000 acções, isto é $2.000.
Assim, ganhamos $650 do nosso lucro menos $2.000, por uma perda de $1.350.
Ganho/perda "dentro do colar
Neste caso, tomamos o ponto médio (53 dólares no vencimento).
Aqui temos uma perda de capital de $1 por acção. Com 1.000 acções, isso é $1.000.
Ganhamos $650 com o lucro líquido das opções e subtraímos os $1.000 (a perda) por uma perda líquida de $350.
Qual é o nosso valor esperado?
Multiplicamos os nossos ganhos/perdas individuais pela probabilidade da sua ocorrência.
Isto dá-nos :
- Acima do limite superior: $650 * 0,50 = $325.
- Abaixo do limite superior: -$1350 * 0,17 = -$229,50.
- Dentro do colar: -$350 * 0,33 = -$115,50.
Somamos estes valores e obtemos menos $20 para o valor esperado.
Assim, se avaliássemos as nossas probabilidades como tal, não teríamos um valor esperado positivo.
Faria sentido que este valor estivesse próximo do ponto de equilíbrio, uma vez que estamos a utilizar em grande parte probabilidades aproximadas sugeridas pelo mercado.
Isto ilustra outra realidade: para ganhar dinheiro nos mercados (para além de uma referência), é preciso apostar contra o consenso e estar certo.
Se pensássemos que as probabilidades associadas a cada uma delas eram antes 0,52, 0,15 e 0,33, então o nosso valor esperado seria positivo - $20.
Outros factores no cálculo do valor esperado
É particularmente importante incluir os custos de transacção.
Isto não é apenas o custo da transacção, mas também a diferença entre o que se negoceia e a qualidade da execução.
Incluem também os custos de financiamento e/ou de contracção de empréstimos.
Muitos títulos e mercados não têm mercados de opções altamente líquidos, o que significa que o spread é muitas vezes bastante grande e que há uma falta de dimensão nos preços de compra e venda.
Isto é particularmente importante para grandes instituições e grandes contas, em geral. Os custos de transacção tendem a aumentar de uma forma não linear.
Os custos de transacção também podem influenciar o que se pretende negociar.
Por exemplo, se estiver a negociar obrigações de média a longa duração, os contratos futuros ZB incluem entre $150.000 e $200.000 de obrigações por contrato, dependendo do preço exacto. Isto significa que pode comprar um único contrato de opção para futuros ZB, enquanto precisa de comprar cerca de 11 contratos por um montante equivalente de TLT (um equivalente ao ETF da obrigação de prazo mais longo).
Os corretores cobram frequentemente de acordo com o volume de contratos. As opções sobre contratos de futuros são geralmente mais caras do que as opções sobre acções e ETFs. Mas os contratos de futuros geralmente incluem um volume maior do subjacente por contrato, o que pode ajudar a reduzir algumas despesas se a dimensão for adequada à sua carteira.
Passando do intuitivo para o explícito
Mesmo que não faça conscientemente os cálculos de valores esperados, fá-los de forma intuitiva a toda a hora.
Se tiver um voo para apanhar, provavelmente parte para o aeroporto com bastante antecedência para se dar a si próprio uma margem de tempo razoável.
Assim, é praticamente impossível perder o seu voo se houver problemas no aeroporto, longas filas de espera, um atraso na segurança, um bilhete ou passaporte mal colocado, ou qualquer outra coisa que possa reduzir esse tempo.
Faz isto porque o lado negativo de perder um voo é elevado em termos de custo monetário, inconveniência e/ou oportunidade perdida.
Optar por não acelerar de carro é outra forma de cálculo do valor esperado. Se as suas hipóteses de obter uma multa por excesso de velocidade forem bastante baixas se mal exceder o limite de velocidade, poderá optar por não conduzir se o risco de obter uma multa for demasiado elevado (ou seja, uma multa, tempo perdido a ser encostado, e possivelmente mais).
Investir não é diferente dos cenários da vida real que enfrentamos e fazemos para maximizar a nossa utilidade e limitar o nosso risco.
Assumir um risco quando se tem muito a ganhar e muito pouco a perder (por exemplo, oportunidades de emprego) é muito semelhante a situações de trading em que se tem um lado negativo limitado e um lado positivo teoricamente ilimitado (por exemplo, comprar opções OTM baratas).
Do mesmo modo, é melhor ser cauteloso quando a perda é muito grande, mesmo que as probabilidades sejam pequenas (por exemplo, um check-up médico se sofrer de um certo sintoma). Isto é semelhante aos traders que vendem opções fora do dinheiro (OTM) por um prémio muito baixo.
Quando o evento de baixa probabilidade ocorre, perdem muitas vezes o prémio que esperavam receber (por vezes centenas ou pior).
À medida que os comerciantes adquirem experiência e sabedoria, estão menos dispostos e menos propensos a negociar coisas sobre as quais não têm fortes convicções.
Ironicamente, os traders novatos tendem a estar bastante confiantes e prontos a saltar, enquanto que os traders experientes são os mais receosos de se enganarem, devido à sua exposição aos mercados ao longo do tempo e aos inevitáveis episódios dolorosos que se seguiram.
Todos os traders precisam de entrar num comércio com consciência da gravidade da situação e da margem de melhoria que têm. É por esta razão que alguns traders optam por nunca entrar numa gama curta (o que basicamente significa que nunca vendem opções).
Embora esta filosofia leve alguns a nunca tirar partido de uma fonte de retorno conhecida como prémio de risco de volatilidade, eles sabem que se nunca forem a uma gama curta, nunca poderão explodir. Para alguns, é uma questão de gestão prudente do risco.
Os traders tendem a confiar no passado recente para preverem o futuro. Podem acontecer coisas que não estão na sua distribuição e não podem ser cotadas no preço.
Se algo nunca aconteceu antes, a única forma de se proteger contra o desconhecido é eliminar completamente o risco de cauda. Portanto, muitos traders que são muito avançados na compreensão do risco e da recompensa tentarão estruturar as suas transacções utilizando opções.
Se venderem opções, eles cobrem-nas com uma posição no subjacente ou outra perna da estrutura da opção. Ao comprar opções, a gestão do risco repousa inteiramente sobre os ombros da contraparte (ou seja, a pessoa que lhe vendeu a opção).
Isto também facilita os cálculos do valor esperado, uma vez que tem um risco negativo claramente definido.
Além disso, para aqueles que definem stop-losses, os mercados caem quando se aproximam da negociação activa durante um período de tempo ou quando há um deslocamento, um evento importante ou um evento de dados. Um stop-loss não mitigará o risco durante períodos anormais.
Conclusão
Se é um trader, jogador profissional ou qualquer outro tipo de decisor profissional, é essencial que conheça o conceito de valor esperado.
Os mercados são semelhantes ao póquer. Deve avaliar constantemente as suas hipóteses de estar certo, a sua recompensa por estar certo, as hipóteses e penalização por estar errado, e como avaliar esta informação com um conhecimento quase sempre imperfeito.
Para tomar as melhores decisões de trading, precisa de compreender o risco e a recompensa.
Qual é o seu risco, quanto pode ganhar com o lado positivo e, muito importante, quais são as probabilidades de estas coisas acontecerem?
Este não é um processo fácil. Para traders diferentes, significa coisas diferentes.
Alguns traders querem saber explicitamente qual é o seu risco negativo por terem opções longas ou por terem uma gestão de risco rigorosa sob a forma de stop-loss.
Eles sabem que dois tipos de risco estão sob controlo: (1) quanto podem perder e (2) que o "risco de ruína" é impossível (podem sempre cobrir a perda).
Os melhores traders limitam as perdas quando estão errados e obtêm grandes lucros quando estão certos.
Para utilizar uma analogia do basebol, não é a sua média de tacadas que conta (a proporção de tacos bem sucedidos em relação ao total de tacos), mas sim a sua percentagem de ganhos (a qualidade geral dos tacos ou a quantidade produzida quando é bem sucedido).
Apostar no que é mais provável nem sempre é a melhor coisa a fazer quando os traders compreendem o valor esperado.
Demasiados visam 'vitórias fáceis' - por exemplo, vender opções OTM - e acabam por eliminar o benefício de um monte de pequenos ganhos com o que acontece quando inevitavelmente um deles se volta atrás, e muitas vezes por várias vezes.
